
分析 (Ⅰ)把n=1代入已知的式子求出a1,当n≥2时把n换成n-1列出式子,再作差化简后求出an;
(Ⅱ)由(Ⅰ)和条件化简得bn,对n进行分类讨论后,利用并项求和法求出数列{bn}的前n项和Tn.
解答 解:(Ⅰ)∵$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}=\frac{n^2}{2}(n∈{N^*})$,①
∴当n=1时,$\frac{1}{a_1}=\frac{1}{2}$,解得a1=2.
当n≥2时,$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{n-1}}}}=\frac{{{{(n-1)}^2}}}{2}(n∈N*)$,②
①-②得,$\frac{1}{a_n}=\frac{n^2}{2}-\frac{{{{(n-1)}^2}}}{2}=\frac{2n-1}{2}$,
解得${a_n}=\frac{2}{2n-1}$,当n=1时也成立,
∴${a_n}=\frac{2}{2n-1}$;
(Ⅱ)由(Ⅰ)可得,${b_n}={(-1)^n}\frac{{4-{a_n}}}{a_n}={(-1)^n}(\frac{4}{a_n}-1)={(-1)^n}(4n-3)$,
当n为偶数时,Tn=-1+5-9+13-17+…+(4n-3)
=(-1+5)+(-9+13)+…+[-(4n-7)+4n-3]
=$4×\frac{n}{2}=2n$,
当n为奇数时,n+1为偶数,
Tn=Tn+1-bn+1=2(n+1)-(4n+1)=-2n+1.
综上,${T_n}=\left\{\begin{array}{l}2n,n为偶数\\-2n+1,n为奇数.\end{array}\right.$.
点评 本题考查数列的通项公式,以及数列求和方法:并项求和法,考查分类讨论思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
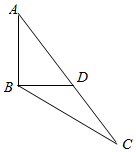 如图,在△ABC中,已知∠ABD=$\frac{π}{2}$,∠CBD=$\frac{π}{6}$,AB=CD=1,则BC=$\root{3}{4}$.
如图,在△ABC中,已知∠ABD=$\frac{π}{2}$,∠CBD=$\frac{π}{6}$,AB=CD=1,则BC=$\root{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com