

分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量:
S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{2014π}{3}$的值,
∵cos$\frac{nπ}{3}$的值以6为周期呈周期性变化,且一个周期内的值的和为0,且2014÷6=335…4,
∴S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{2014π}{3}$=335×0+cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+cos$\frac{4π}{3}$=-$\frac{3}{2}$,
故答案为:-$\frac{3}{2}$.
点评 本题主要考查了循环结构的程序框图的应用,考查了余弦函数的图象和性质,模拟执行程序框图,得到程序的功能是解题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [0,1) | C. | [1,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2) | B. | (-2,-2) | C. | (2,2)或(-2,-2) | D. | (2$\sqrt{2}$,2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
在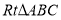 中,
中,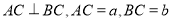 ,则
,则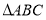 的外接圆半径
的外接圆半径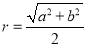 ;类比到空间,若三棱锥
;类比到空间,若三棱锥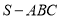 的三条侧棱
的三条侧棱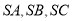 两两互相垂直,且长度分别为
两两互相垂直,且长度分别为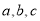 ,则三棱锥
,则三棱锥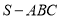 的外接球的半径
的外接球的半径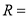 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com