
���� ��������֪�æεĿ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ����г��εķֲ��С������ѧ����E�Σ������ɣ�I�������⻯��an���������|an|���ɵȲ����е�ǰn���ʽ���Sn��
��� �⣺����������æεĿ���ȡֵΪ0��1��2��3------1��
$P����=0��=\frac{1}{2}��\frac{2}{3}��1-t��=\frac{2-2t}{6}$-------2
$P����=1��=\frac{1}{2}��\frac{2}{3}��1-t��+\frac{1}{2}��\frac{1}{3}��1-t��+\frac{1}{2}��\frac{2}{3}t=\frac{3-t}{6}$--------3
$P����=2��=\frac{1}{2}��\frac{1}{3}��1-t��+\frac{1}{2}��\frac{1}{3}t+\frac{1}{2}��\frac{2}{3}t$=$\frac{1+2t}{6}$-------4
$P����=3��=\frac{1}{2}��\frac{1}{3}t=\frac{1}{6}t$-------5��
���Ԧεķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1-t}{3}$ | $\frac{3-t}{6}$ | $\frac{1+2t}{6}$ | $\frac{t}{6}$ |
���� ���⿼����ɢ����������ķֲ��С���ѧ���������Լ��Ȳ����е�ǰn���ʽ�����е��⣬


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Сֵ�����������Ž⣬���ֵֻ��һ�����Ž� | |
| B�� | ���ֵ����Сֵ�������������Ž� | |
| C�� | ���ֵ�����������Ž⣬��Сֵֻ��һ�����Ž� | |
| D�� | ���ֵ����Сֵ��ֻ��һ�����Ž� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��㶫��Զ���и�һ��ѧ���¿�һ��ѧ�Ծ��������棩 ���ͣ������
���г����飬ij���в���һ��С��Ʒ�ڹ�ȥ��20���ڵ�����������������۸�Ԫ����Ϊʱ��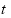 ���죩�ĺ����������������������㺯��
���죩�ĺ����������������������㺯��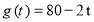 ���������������ۼ۸����������
���������������ۼ۸���������� ��Ԫ����
��Ԫ����
��1����д��������Ʒ�������۶�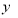 ��ʱ��
��ʱ��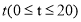 �ĺ�������ʽ��
�ĺ�������ʽ��
��2���������Ʒ�������۶�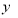 �����ֵ����Сֵ��
�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com