
分析 根据倾斜角为α的直线l与直线x+2y-3=0垂直,得到tanα=2,再根据向量的数量积和模即可求出.
解答 解:倾斜角为α的直线l与直线x+2y-3=0垂直,
∴tanα=2,
∴$cosα=\frac{{\sqrt{5}}}{5}$,
∵|${\overrightarrow a$+$\overrightarrow b}$|2=|${\overrightarrow a$|2+|$\overrightarrow b}$|2+2${\overrightarrow a$•$\overrightarrow b}$=|${\overrightarrow a$|2+|$\overrightarrow b}$|2+2|${\overrightarrow a$|•|$\overrightarrow b}$|•cosα=8,
∴${|{\overrightarrow b}|^2}+2|{\overrightarrow b}|-3=0$,
解得$|{\overrightarrow b}|=1$.
故答案为:1.
点评 本题考查了向量的数量积和向量的模,以及直线的倾斜率问题,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|-1<x<1} | C. | {x|0<x<1} | D. | {x|-2<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
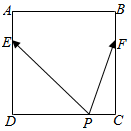 如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.
如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.| A. | 2 | B. | 4 | C. | 6 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值2,无最小值 | B. | 有最小值2,无最大值 | ||
| C. | 有最小值$\frac{1}{2}$,最大值2 | D. | 既无最小值,也无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com