
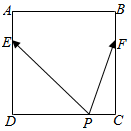
 如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.
如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.| A. | 2 | B. | 4 | C. | 6 | D. | 0 |
分析 由题意可得DE=4,AE=2,CF=4,BF=2,分类讨论P点的位置,分别求得$\overrightarrow{PE}$•$\overrightarrow{PF}$的范围,从而得出结论
解答 解:由正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF,
可得DE=4,AE=2,CF=4,BF=2.
若P在AB上,$\overrightarrow{PE}•\overrightarrow{PF}=(\overrightarrow{PA}+\overrightarrow{AE})(\overrightarrow{PB}+\overrightarrow{BF})=\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{AE}•\overrightarrow{BF}∈[-5,4]$;
若P在CD上,$\overrightarrow{PE}•\overrightarrow{PF}=(\overrightarrow{PD}+\overrightarrow{DE})(\overrightarrow{PC}+\overrightarrow{CF})=\overrightarrow{PD}•\overrightarrow{PC}+\overrightarrow{DE}•\overrightarrow{CF}∈[7,16]$;
若P在AE上,$\overrightarrow{PE}•\overrightarrow{PF}=\overrightarrow{PE•(}\overrightarrow{PA}+\overrightarrow{AB}+\overrightarrow{BF})=\overrightarrow{PE}•\overrightarrow{PA}+\overrightarrow{PE}•\overrightarrow{BF}∈[0,4]$;
同理,P在BF上时也有$\overrightarrow{PE}•\overrightarrow{PF}∈[0,4]$;
若P在DE上,$\overrightarrow{PE}•\overrightarrow{PF}=\overrightarrow{PE•(}\overrightarrow{PD}+\overrightarrow{DC}+\overrightarrow{CF})=\overrightarrow{PE}•\overrightarrow{PD}+\overrightarrow{PE}•\overrightarrow{CF}∈[0,16]$;
同理,P在CF上时也有$\overrightarrow{PE}•\overrightarrow{PF}∈[0,16]$,
所以,综上可知当λ∈(7,16)时,有且只有4个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立.
故选:B
点评 本题主要考查两个向量的加减法及其几何意义,两个向量的数量积公式,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
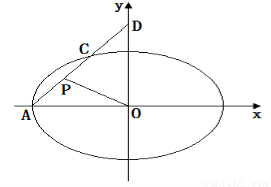
过椭圆 的左顶点
的左顶点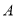 作斜率为
作斜率为 的直线
的直线 交椭圆于点
交椭圆于点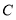 ,交
,交 轴于点
轴于点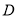 ,
, 为
为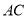 中点,定点
中点,定点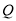 满足:对于任意的
满足:对于任意的 都有
都有 ,则
,则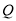 点的坐标为 .
点的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com