
分析 (1)设P(x,y),A(x1,0),B(0,y1),由$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$把A、B的坐标用P的坐标表示,结合|AB|=3,求得动点P的轨迹C的方程;
(2)假设存在直线l满足条件,由直线l过点$M(-\sqrt{3},0)$,而点M,N是椭圆C:$\frac{x^2}{4}+{y^2}=1$的左右焦点,由椭圆的定义得△DEN的周长为8,再由△DEN的内切圆的面积为$\frac{3π}{16}$,得△DEN的内切圆的半径,联立直线方程和椭圆方程,利用根与系数的关系及弦长公式解得m=0或m=±$2\sqrt{2}$.说明存在直线l.
解答 解:(1)设P(x,y),A(x1,0),B(0,y1),
则$\overrightarrow{AP}=(x-{x_1},y),\overrightarrow{AB}=(-{x_1},{y_1})$-------(2分)
由$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}$,有$\left\{\begin{array}{l}x-{x_1}=-\frac{1}{3}{x_1}\\ y=\frac{1}{3}{y_1}\end{array}\right.$,得$\left\{\begin{array}{l}{x_1}=\frac{3}{2}x\\{y_1}=3y\end{array}\right.$,--------------(4分)
由|AB|=3,得$x_1^2+y_1^2=9$,--------------(5分)
∴${(\frac{3}{2}x)^2}+{(3y)^2}=9$,即$\frac{x^2}{4}+{y^2}=1$,
∴动点P的轨迹C的方程为$\frac{x^2}{4}+{y^2}=1$;--------------(6分)
(2)假设存在直线l满足条件,∵直线$l:x=my-\sqrt{3}$过点$M(-\sqrt{3},0)$,
而点M,N是椭圆C:$\frac{x^2}{4}+{y^2}=1$的左右焦点,
∴由椭圆的定义得,△DEN的周长为8,-------------(7分)
由△DEN的内切圆的面积为$\frac{3π}{16}$,得△DEN的内切圆的半径为$\frac{{\sqrt{3}}}{4}$;
设点D(x1,y1),E(x2,y2),则△DEN的面积为$\frac{1}{2}×|MN|×|{y_1}-{y_2}|$=$\frac{1}{2}×8×\frac{{\sqrt{3}}}{4}$;
∴|y1-y2|=1;-------------(9分)
由$\left\{\begin{array}{l}x=my-\sqrt{3}\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,消去x并整理得$({m^2}+4){y^2}-2\sqrt{3}my-1=0$.
则$|{y_1}-{y_2}|=\frac{{\sqrt{△}}}{a}=\frac{{\sqrt{16{m^2}+16}}}{{{m^2}+4}}=1$,-------------(11分)
解得m=0或m=±$2\sqrt{2}$.
故存在直线l,且m的值为0,$-2\sqrt{2}$或$2\sqrt{2}$.-------------(12分)
点评 本题考查利用代入法求曲线的方程,考查了直线与圆锥曲线位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | [0,1) | C. | [1,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | B. | -$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
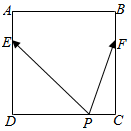 如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.
如图,正方形ABCD的边长为6,点E,F分别在边AD,BC上,且DE=2AE,CF=2BF.若有λ∈(7,16),则在正方形的四条边上,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立的点P有( )个.| A. | 2 | B. | 4 | C. | 6 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2) | B. | (-2,-2) | C. | (2,2)或(-2,-2) | D. | (2$\sqrt{2}$,2$\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com