
分析 (Ⅰ)由题意可知:a=2c,$\frac{2{b}^{2}}{a}$=3,且a2=b2+c2,即可求得a和b的值,求得椭圆方程;
(Ⅱ)分类讨论,当直线l不垂直与x轴时,设直线方程,代入椭圆方程,由韦达定理及直线的斜率公式,即可求得kTR+kTS=0,即可证明直线TS与TR的斜率之和为定值.
解答 解:(Ⅰ)由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,则a=2c,将x=c代入椭圆方程,
解得:y=±$\frac{{b}^{2}}{a}$,|RS|=$\frac{2{b}^{2}}{a}$=3,
由a2=b2+c2,则a=2,b=$\sqrt{3}$,c=1,
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)证明:当直线l垂直与x轴时,显然直线TS与TR的斜率之和为0,
当直线l不垂直与x轴时,设直线l的方程为y=k(x-1),R(x1,y1),S(x2,y2),
$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}-12=0}\end{array}\right.$,整理得:(3+4k2)x2-8k2x+4k2x+4k2-12=0,
△=64k4-4(3+4k2)(4k2-12)=k2+1>0恒成立,
x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
由kTR+kTS=$\frac{{y}_{1}}{{x}_{1}-4}$+$\frac{{y}_{2}}{{x}_{2}-4}$,TR,TS的斜率存在,
由R,S两点的直线y=k(x-1),
故y1=k(x1-1),y2=k(x2-1),
则$\frac{k({x}_{1}-1)({x}_{2}-4)+k({x}_{2}-1)({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$=$\frac{k[2{x}_{1}{x}_{2}-5({x}_{1}+{x}_{2})+8]}{({x}_{1}-4)({x}_{2}-4)}$,
由2x1x2-5(x1+x2)+8=2×$\frac{4{k}^{2}-12}{3+4{k}^{2}}$-5×$\frac{8{k}^{2}}{3+4{k}^{2}}$+8=0,
∴kTR+kTS=0,
∴直线TS与TR的斜率之和为0,
综上所述,直线TS与TR的斜率之和为为定值,定值为0.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{1}{2})$ | B. | $(1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},1)$ | D. | $(-\frac{1}{2},-1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 5 | B. | 12 | C. | 25 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
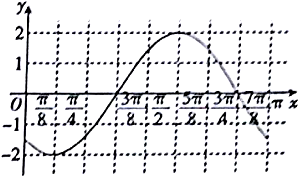 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com