
| A. | $\frac{2}{9}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{6}$ | D. | -$\frac{2}{9}$ |
分析 根据三角形法则分别将$\overrightarrow{MA}、\overrightarrow{MB}$用$\overrightarrow{CA}$、$\overrightarrow{CB}$表示出来,根据向量的数量积运算法则计算出结果即可.
解答 解:∵$\overrightarrow{CM}$=$\frac{1}{3}$$\overrightarrow{CB}$+$\frac{1}{2}\overrightarrow{CA}$,
∴$\overrightarrow{MA}=\overrightarrow{CA}-\overrightarrow{CM}$=$\frac{1}{2}\overrightarrow{CA}-\frac{1}{3}\overrightarrow{CB}$,$\overrightarrow{MB}=\overrightarrow{CB}-\overrightarrow{CM}$=$\frac{2}{3}\overrightarrow{CB}-\frac{1}{2}\overrightarrow{CA}$,
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=-$\frac{1}{4}{\overrightarrow{CA}}^{2}$+$\frac{1}{2}\overrightarrow{CA}•\overrightarrow{CB}$-$\frac{2}{9}{\overrightarrow{CB}}^{2}$,
又△ABC为边长为1的等边三角形,
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=-$\frac{1}{4}+\frac{1}{4}-\frac{2}{9}=-\frac{2}{9}$.
故选:D.
点评 本题主要考查了向量的三角形法则和数量积的运算,属于中档题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-1) | B. | [-3,-1] | C. | (-∞,-3]∪[-1,+∞) | D. | (-∞,-3)∪(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
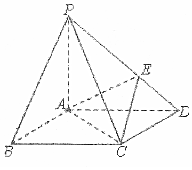 在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.
在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-∞,-2018) | C. | (-2018,0) | D. | (-2016,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<0} | B. | {x|0<x≤1} | C. | {x|0≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,+∞) | C. | (-∞,1) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com