考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:圆锥曲线中的最值与范围问题
分析:(1)连接AC,BD交于点O,以OA为x轴正方向,以OB为y轴正方向,OP为z轴建立空间直角坐标系.利用向量法能证明MN⊥AD.
(2)设
=λ,得M(λ,0,1-λ),
=(λ,-1,1-λ),
=(0,-2,0),分别求出平面MBD的法向量和平面ABD的法向量,利用向量法解得
λ=,由此能求出线段MN的长度.
解答:
(本小题满分10分)
(1)证明:连接AC,BD交于点O,以OA为x轴正方向,以OB为y轴正方向,
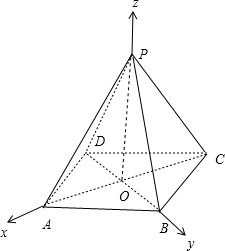
OP为z轴建立空间直角坐标系.
∵PA=AB=
,则A(1,0,0),B(0,1,0),
D(0,-1,0),P(0,0,1).
=,得N(0,
,0),
由
=,得M(
,0,
),
=(-,,-),
=(-1,-1,0),
∵
•=0,∴MN⊥AD.
(2)∵M在PA上,设
=λ,得M(λ,0,1-λ),
∴
=(λ,-1,1-λ),
=(0,-2,0),
设平面MBD的法向量
=(x,y,z),
由
,得
,
取z=λ,得
=(λ-1,0,λ),
∵平面ABD的法向量为
=(0,0,1),二面角M-BD-A的大小为
,
∴cos
=|
|,即
=,解得
λ=,
∴M(
,0,),N(0,
,0),
∴|MN|=
=
.
点评:本题考查异面直线垂直的证明,考查线段长的求法,解题时要认真审题,注意向量法的合理运用.

 如图,在正四棱锥P-ABCD中,PA=AB=
如图,在正四棱锥P-ABCD中,PA=AB=


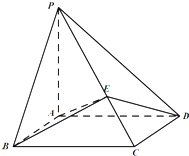 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=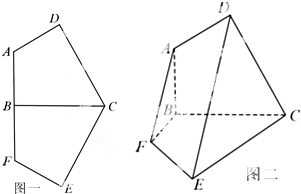 已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=