
【题目】已知各项为正的数列![]() 满足:
满足: ![]() ,
, ![]() (
(![]() ).
).
(1)求![]() ;
;
(2)证明: ![]() (
(![]() );
);
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: 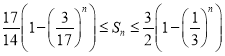 .
.
【答案】(1) ![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)根据条件递推公式: ![]() ,
, ![]() ,依次推导
,依次推导![]() 。(2)要证明
。(2)要证明![]() ,故应由条件得到
,故应由条件得到![]() ,所以将条件
,所以将条件![]() 两边减去2得
两边减去2得![]() ,将右边通分,进而化为
,将右边通分,进而化为![]() 由条件
由条件![]() ,可得
,可得![]() 。所以
。所以![]() 与
与![]() 异号。得到结论。(3)由(2)知
异号。得到结论。(3)由(2)知![]() 与
与![]() 异号,要求数列
异号,要求数列![]() 的前
的前![]() 项和为
项和为![]() ,故应找数列
,故应找数列![]() 的间隔项的关系。由(2)知
的间隔项的关系。由(2)知![]() ,利用此关系式将式子中的
,利用此关系式将式子中的![]() 化成
化成 ![]() ,并化简可得
,并化简可得![]()
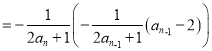
![]() (
(![]() )。
)。
要找数列![]() 的间隔项的关系,再变为
的间隔项的关系,再变为![]() (
(![]() )。应判断式子右边的范围。由
)。应判断式子右边的范围。由![]() 可得
可得 ![]() (
(![]() )。进而得左边的范围
)。进而得左边的范围![]() (
(![]() )。所以
)。所以![]() 与
与![]() 同号。先求数列
同号。先求数列![]() 前两项的范围,
前两项的范围, ![]() 。进而可得数列
。进而可得数列![]() 奇数项、偶数项的正负。即当
奇数项、偶数项的正负。即当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() 。再分奇偶判断数列
。再分奇偶判断数列![]() 奇数、偶数项的范围及单调性。可得
奇数、偶数项的范围及单调性。可得![]() ,结合条件可得
,结合条件可得![]() 。由(2)知
。由(2)知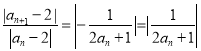 ,故先求右边的范围
,故先求右边的范围
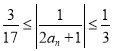 ,进而得
,进而得![]() 。利用累乘法可得
。利用累乘法可得![]() 。再用等比数列求和公式可得
。再用等比数列求和公式可得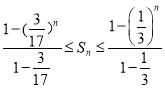 。化简可得
。化简可得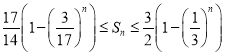 。
。
详解:(1)![]()
![]()
![]()
(2)![]()
![]()
![]()
![]() 与
与![]() 异号
异号
![]()
(3)由(2)知![]()
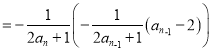 (
(![]() )
)
![]() (
(![]() )
)
所以![]() (
(![]() )
)
![]()
![]() (
(![]() )
)
![]() (
(![]() )
)
![]() 与
与![]() 同号
同号
又![]()
![]() 当
当![]() 时,
时, ![]()
当![]() 时,
时, ![]()
①当![]() 且
且![]() 为偶数时
为偶数时
![]()
![]()
![]()
![]()
![]() 数列
数列![]() 递增且各项都小于2
递增且各项都小于2
②当![]() 且
且![]() 为奇数时
为奇数时
![]()
![]()
![]()
![]()
![]() 数列
数列![]() 递减且各项都大于2
递减且各项都大于2
![]() 由①②知,
由①②知, ![]()
![]()
由(2)知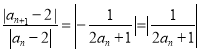
![]()
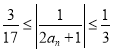
![]()
![]()
又
![]()
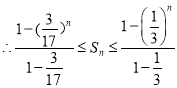
![]()


科目:高中数学 来源: 题型:
【题目】如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F. (Ⅰ)求证:C、D、G、E四点共圆.
(Ⅱ)若F为EB的三等分点且靠近E,EG=1,GA=3,求线段CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
(1)cosα≠0是 ![]() 的充分必要条件
的充分必要条件
(2)f(x)=|sinx|+|cosx|,则f(x)最小正周期是π
(3)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变
(4)设随机变量ζ服从正态分布N(0,1),若P(ζ>1)=p,则 ![]() .
.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. (I)证明:AE⊥PD;
(II)H是PD上的动点,EH与平面PAD所成的最大角为45°,求二面角E﹣AF﹣C的正切值.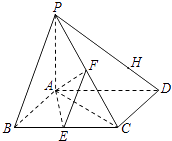
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 把![]() 上所有的点向右平移
上所有的点向右平移![]() 个单位长度,再把所有图象上各点的横坐标缩短到原来的
个单位长度,再把所有图象上各点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到曲线
倍(纵坐标不变),得到曲线![]()
B. 把![]() 上所有点向左平移
上所有点向左平移![]() 个单位长度,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变),得到曲线
个单位长度,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变),得到曲线![]()
C. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍(纵坐标不变),再把所得图象上所有的点向左平移
倍(纵坐标不变),再把所得图象上所有的点向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的3倍(纵坐标不变),再把所得图象上所有的点向左平移
上各点的横坐标伸长到原来的3倍(纵坐标不变),再把所得图象上所有的点向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市大学生创业孵化基地某公司生产一种“儒风邹城”特色的旅游商品.该公司年固定成本为10万元,每生产千件需另投入2.7万元;设该公司年内共生产该旅游商品![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且满足函数关系:
万元,且满足函数关系: .
.
(Ⅰ)写出年利润![]() (万元)关于该旅游商品
(万元)关于该旅游商品![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在该旅游商品的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列类比推理命题(其中![]() 为有理数集,
为有理数集,![]() 为实数集,
为实数集,![]() 为复数集),其中类比结论正确的是( )
为复数集),其中类比结论正确的是( )
A. “若![]() ,则
,则![]() ”类比推出“若
”类比推出“若![]() ,则
,则![]() ”.
”.
B. ![]() 类比推出
类比推出![]()
C. ![]() 类比推出
类比推出![]()
D. “若![]() ,则
,则![]() ”类比推出“若
”类比推出“若![]() ,则
,则![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com