已知数列{an}的首项a1=5,an+1=2an+1.
(1)证明:数列{an+1}是等比数列;
(2)若数列{nan}的前n项和为Tn,试比较2Tn与23n2-13n的大小.
解:(1)∵a
n+1=2a
n+1,∴a
n+1+1=2a
n+2=2(a
n+1),
又∵a
1=5,得a
1+1=6≠0
∴
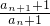
=2,即数列{a
n+1}是以6为首项,公比等于2的等比数列.…(5分)
(2)由(Ⅰ)知a
n+1=6×2
n-1=3×2
n,所以a
n=3×2
n-1…(7分)
从而T
n=(3×2-1)+2(3×2
2-1)+3(3×2
3-1)+…+n(3×2
n-1)
=3(2+2×2
2+3×2
3+…+n×2
n)-(1+2+3+…+n)
令P
n=2+2×2
2+3×2
3+…+n×2
n,得2P
n=2
2+2×2
3+3×2
4+…+n×2
n+1,
相减得,P
n=n×2
n+1-(2
2+2
3+2
4+…+2
n)-2=(n-1)2
n+1+2,
∴T
n=3[(n-1)2
n+1+2]-

(n
2+n)=3(n-1)2
n+1-

(n
2+n-12)…(9分)
所以2T
n-(23n
2-13n)=12(n-1)2
n-12(2n
2-n-1)=12(n-1)(2
n-2n-1)…①
当n=1时,①式等于0,所以2T
n=23n
2-13n;
当n=2时,①式等于-12<0,所以2T
n<23n
2-13n
当n≥3时,n-1>0且2
n>2n+1,所以,①式符号为正,从而2T
n>23n
2-13n.…(13分)
分析:(1)根据已知等式变形可得
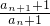
=2,结合首项a
1=5,得列{a
n+1}是以6为首项,公比等于2的等比数列.
(2)由等比数列的通项公式和错位相减法求和,结合等差数列的求和公式,算出T
n=3(n-1)2
n+1-

(n
2+n-12),将此代入2T
n,再与23n
2-13n作差因式分解,最后再对n进行讨论,不难得出2T
n与23n
2-13n的大小.
点评:本题给出数列的递推公式,求数列的通项并且比较两个式子的大小,着重考查等比数列、错位相减法,考查灵活运用知识解决问题的能力,属于中档题.

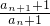 =2,即数列{an+1}是以6为首项,公比等于2的等比数列.…(5分)
=2,即数列{an+1}是以6为首项,公比等于2的等比数列.…(5分) (n2+n)=3(n-1)2n+1-
(n2+n)=3(n-1)2n+1- (n2+n-12)…(9分)
(n2+n-12)…(9分)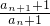 =2,结合首项a1=5,得列{an+1}是以6为首项,公比等于2的等比数列.
=2,结合首项a1=5,得列{an+1}是以6为首项,公比等于2的等比数列. (n2+n-12),将此代入2Tn,再与23n2-13n作差因式分解,最后再对n进行讨论,不难得出2Tn与23n2-13n的大小.
(n2+n-12),将此代入2Tn,再与23n2-13n作差因式分解,最后再对n进行讨论,不难得出2Tn与23n2-13n的大小.

 小题狂做系列答案
小题狂做系列答案