
(2005•北京)已知函数f(x)=﹣x3+3x2+9x+a.
(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)若f(x)在区间[﹣2,2]上的最大值为20,求它在该区间上的最小值.
(Ⅰ)(﹣∞,﹣1),(3,+∞).
(Ⅱ)﹣7
【解析】
试题分析:(Ⅰ)先求出函数f(x)的导函数f′(x),然后令f′(x)<0,解得的区间即为函数f(x)的单调递减区间;
(Ⅱ)先求出端点的函数值f(﹣2)与f(2),比较f(2)与f(﹣2)的大小,然后根据函数f(x)在[﹣1,2]上单调递增,在[﹣2,﹣1]上单调递减,得到f(2)和f(﹣1)分别是f(x)在区间[﹣2,2]上的最大值和最小值,建立等式关系求出a,从而求出函数f(x)在区间[﹣2,2]上的最小值.
【解析】
(Ⅰ)f′(x)=﹣3x2+6x+9.
令f′(x)<0,解得x<﹣1或x>3,
所以函数f(x)的单调递减区间为(﹣∞,﹣1),(3,+∞).
(Ⅱ)因为f(﹣2)=8+12﹣18+a=2+a,f(2)=﹣8+12+18+a=22+a,
所以f(2)>f(﹣2).
因为在(﹣1,3)上f′(x)>0,所以f(x)在[﹣1,2]上单调递增,
又由于f(x)在[﹣2,﹣1]上单调递减,
因此f(2)和f(﹣1)分别是f(x)在区间[﹣2,2]上的最大值和最小值,于是有22+a=20,解得a=﹣2.
故f(x)=﹣x3+3x2+9x﹣2,因此f(﹣1)=1+3﹣9﹣2=﹣7,
即函数f(x)在区间[﹣2,2]上的最小值为﹣7.


科目:高中数学 来源:[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷(解析版) 题型:解答题
已知集合P={x|x2+x﹣6=0},M={x|mx﹣1=0},若M?P,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
做一个无盖的圆柱形水桶,若要使体积是27π,且用料最省,则圆柱的底面半径为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
某公司生产某种产品,固定成本为20000元,每生产一单位产品,成本增加100元,已知总收益R与年产量x的关系为R=R(x)=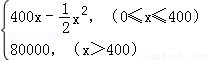 ,则总利润最大时,每年生产的产品数量是 .
,则总利润最大时,每年生产的产品数量是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:填空题
(3分)若函数f(x)=ax2+4x﹣3在[0,2]上有最大值f(2),则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:填空题
(3分)设函数f(x)在区间[a,b]上满足f′(x)<0,则函数f(x)在区间[a,b]上的最小值为 ,最大值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷(解析版) 题型:解答题
已知函数f(x)=x3,求证:函数在任意区间[a,a+b]上的平均变化率都是正数.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:填空题
设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com