练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （3分）设函数f（x）在区间[a，b]上满足f′（x）＜0，则函数f（x）在区间[a，b]上的最小值为 ，最大值为 ．

     

    f（b） f（a）

    【解析】

    试题分析：先利用导数的符号判断函数f（x）在区间[a，b]上的单调性，再求出f（x）在区间[a，b]上的最大值和最小值即可．

    解析：由f′（x）＜0，可知f（x）在区间[a，b]上为单调减函数，则最小值为f（b），最大值为f（a）．

    故答案为：f（b） f（a）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年苏教版必修三 2.3 总体特征数的估计练习卷（解析版） 题型：选择题

    在统计中，样本的标准差可以近似地反映总体的（ ）

    A.平均状态 B.频率分布 C.波动大小 D.最大值和最小值

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷（解析版） 题型：解答题

    如图所示，设铁路AB=50，B、C之间距离为10，现将货物从A运往C，已知单位距离铁路费用为2，公路费用为4，问在AB上何处修筑公路至C，可使运费由A到C最省？

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷（解析版） 题型：解答题

    （2005•北京）已知函数f（x）=﹣x3+3x2+9x+a．

    （Ⅰ）求f（x）的单调递减区间；

    （Ⅱ）若f（x）在区间[﹣2，2]上的最大值为20，求它在该区间上的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷（解析版） 题型：填空题

    （3分）函数f（x）=xlnx在（0，+∞）上的最小值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.2导数的运算练习卷（解析版） 题型：填空题

    设μ∈R，函数f（x）=ex+的导函数是f′（x），且f′（x）是奇函数，若曲线y=f（x）的一条切线的斜率是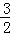，则该切点的横坐标是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.2导数的运算练习卷（解析版） 题型：填空题

    已知直线y=kx与曲线y=lnx相切，则k= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷（解析版） 题型：填空题

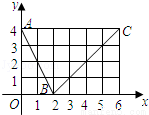
    如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标为（0，4），（2，0），（6，4），则f（f（0））= ；函数f（x）在x=1处导数f′（1）= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.1 椭圆练习卷（解析版） 题型：解答题

    已知直线l：y=kx+1与椭圆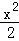+y2=1交于M、N两点，且|MN|=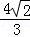．求直线l的方程．

     

    查看答案和解析>>

    同步练习册答案