
设μ∈R,函数f(x)=ex+ 的导函数是f′(x),且f′(x)是奇函数,若曲线y=f(x)的一条切线的斜率是
的导函数是f′(x),且f′(x)是奇函数,若曲线y=f(x)的一条切线的斜率是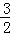 ,则该切点的横坐标是 .
,则该切点的横坐标是 .
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
做一个无盖的圆柱形水桶,若要使体积是27π,且用料最省,则圆柱的底面半径为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:填空题
(3分)若函数f(x)=ax2+4x﹣3在[0,2]上有最大值f(2),则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:填空题
(3分)设函数f(x)在区间[a,b]上满足f′(x)<0,则函数f(x)在区间[a,b]上的最小值为 ,最大值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷(解析版) 题型:解答题
已知函数f(x)=x3,求证:函数在任意区间[a,a+b]上的平均变化率都是正数.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:解答题
中国跳水运动员进行10 m跳台跳水训练时,身体(看成一点)在空中的运动路线为如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10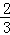 m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
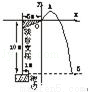
(1)求这条抛物线的解析式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3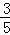 m,问此次跳水会不会失误?并通过计算说明理由.
m,问此次跳水会不会失误?并通过计算说明理由.
(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)椭圆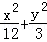 =1的焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是( )
=1的焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是( )
A.±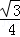 B.±
B.±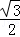 C.±
C.±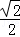 D.±
D.±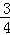
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com