(-

,-2)∪(-2,1)
分析:令t=sinx,当x∈[π,

]时,x与t一一对应,由题意可得直线y=a和曲线y=2t
2+t-2在[-

,1]上有两个交点,由此求得a的范围. 当x∈(0,π),且x≠

时,有2个x与一个t值对应,直线y=a和曲线y=2t
2+t-2在[-

,1)上有一个交点,结合图象求出实数a的取值范围. 再把以上2个a的取值范围取并集,即得所求.
解答:
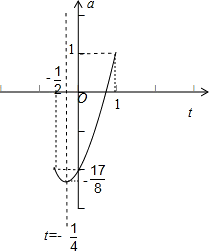
解:由题意,方程可变为a=-2cos
2x+sinx,令t=sinx,
由0<x≤

,可得 t∈[-

,1].
①当x∈[π,

]时,t∈[-

,0],此时,x与t一一对应.
由题意可得,关于t的方程a=2t
2+t-2,当t∈[-

,0]应有2个实数根,
即直线y=a和函数y=2t
2+t-2,当t∈[-

,0]应有2个交点.
当t=-

时,y=2t
2+t-2有最小值-

. 当t=-

或0时,a=2t
2+t-2=-2.
此时,应有 a∈(-

,-2].
但当a=-2时,t=-

或0,在区间[0,

]上,对应x=0 或π或

,
关于x的方程2cos
2x-sinx+a=0在区间[0,

]上有3个实数根,
故不满足条件,应舍去,故 a∈(-

,-2).
②当x∈(0,π),且x≠

时,有2个x与一个t值对应.
故由题意可得,关于t的方程a=2t
2+t-2,当t∈(0,1)有一个实数根,
即直线y=a和曲线y=2t
2+t-2在(0,1)上有一个交点,如图所示:
此时,a∈(-2,1).
综上可得,实数a的取值范围是 (-

,-2)∪(-2,1),
故答案为 (-

,-2)∪(-2,1).
点评:本题的考点是复合函数的单调性,考查根据复合三角函数的单调性求值域,本题求参数范围的题转化为求函数的值域是解此类题的常用技巧,属于中档题.

 ]上恰好有两个不等实根,则实数a的取值范围是________.
]上恰好有两个不等实根,则实数a的取值范围是________. ,-2)∪(-2,1)
,-2)∪(-2,1) ]时,x与t一一对应,由题意可得直线y=a和曲线y=2t2+t-2在[-
]时,x与t一一对应,由题意可得直线y=a和曲线y=2t2+t-2在[- ,1]上有两个交点,由此求得a的范围. 当x∈(0,π),且x≠
,1]上有两个交点,由此求得a的范围. 当x∈(0,π),且x≠ 时,有2个x与一个t值对应,直线y=a和曲线y=2t2+t-2在[-
时,有2个x与一个t值对应,直线y=a和曲线y=2t2+t-2在[- ,1)上有一个交点,结合图象求出实数a的取值范围. 再把以上2个a的取值范围取并集,即得所求.
,1)上有一个交点,结合图象求出实数a的取值范围. 再把以上2个a的取值范围取并集,即得所求.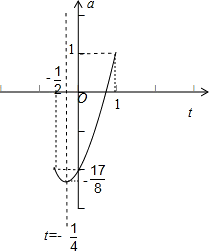 解:由题意,方程可变为a=-2cos2x+sinx,令t=sinx,
解:由题意,方程可变为a=-2cos2x+sinx,令t=sinx, ,可得 t∈[-
,可得 t∈[- ,1].
,1]. ]时,t∈[-
]时,t∈[- ,0],此时,x与t一一对应.
,0],此时,x与t一一对应. ,0]应有2个实数根,
,0]应有2个实数根, ,0]应有2个交点.
,0]应有2个交点. 时,y=2t2+t-2有最小值-
时,y=2t2+t-2有最小值- . 当t=-
. 当t=- 或0时,a=2t2+t-2=-2.
或0时,a=2t2+t-2=-2. ,-2].
,-2]. 或0,在区间[0,
或0,在区间[0, ]上,对应x=0 或π或
]上,对应x=0 或π或 ,
, ]上有3个实数根,
]上有3个实数根, ,-2).
,-2). 时,有2个x与一个t值对应.
时,有2个x与一个t值对应. ,-2)∪(-2,1),
,-2)∪(-2,1), ,-2)∪(-2,1).
,-2)∪(-2,1).

 阅读快车系列答案
阅读快车系列答案