
r2-(
|
| |2a-4| | ||
|
| a2+a2 |
| 2a2 |
| 2 |
r2-(
|
| |3-k| | ||
|
| 4 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| e-1 |
| ax2 |
| e2 |
| (1+2a-ea)x |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
| x1x2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
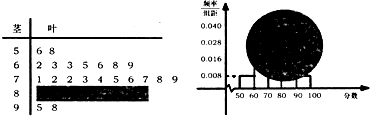 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
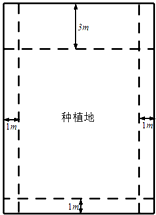 某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| π |
| 2 |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com