考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数判断函数的单调性,求得函数的最小值,故由题意得只要函数的最小值小于0即可,注意对a分类讨论;
(2)记
h(x)=f′(x)=2x-a-,则
h′(x)=2+>0,所以f'(x)为(0,+∞)上的增函数.要证
<x0<,只要证
f′()<f′(x0)<f′().利用导数证明即可.
解答:
解:(Ⅰ)
f′(x)=…(1分)
当x→0时,f(x)→+∞,当x→+∞时,f(x)→+∞.
当a>0时,f(x)在(0,a)上递减,在(a,+∞)上递增,
所以f(x)的最小值为f(a)=-a
2lna,由-a
2lna<0解得a>1.…(4分)
当a<0时,f(x)在
(0,-)上递减,在
(-,+∞)上递增,
所以f(x)的最小值为
f(-)=a2-a2ln(-),
由
a2-a2ln(-)<0解得
a<-2e.
所以a的取值范围为
a<-2e或a>1…(7分)
(Ⅱ)记
h(x)=f′(x)=2x-a-,则
h′(x)=2+>0,…(8分)
所以f'(x)为(0,+∞)上的增函数.
要证
<x0<,
只要证
f′()<f′(x0)<f′().…(9分)
不妨设x
1<x
2f′(x0)==(x1+x2)-a-a2f′()-f′(x0)=(ln-2)设
F(t)=lnt-2(t∈(0,1]),则
F′(x)=≥0∴F(t)在(0,1]为增函数.∴当t∈(0,1)时,F(t)<F(1)=0
令
t=得
ln-2<0,又
<0,
∴
f′()-f′(x0)>0,即
f′()>f′(x0)…(12分)
f′()-f′(x0)=2-(x1+x2)+[ln-(-)]设
G(t)=2lnt-(t-)(t∈(0,1]),则
G′(t)=-<0∴G(t)在(0,1]为减函数.∴当t∈(0,1)时,G(t)>G(1)=0
令
t=得
ln-(-)>0,又
<0,
2-(x1+x2)<0所以
f′()-f′(x0)<0,即
f′()<f′(x0)所以
f′()<f′(x0)<f′()即
<x0<.…(14分)
点评:本题主要考查利用导数研究函数的单调性,求函数的最值等知识,考查学生分析问题,解决问题的能力及运算求解能力,综合性逻辑性强,属难题.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案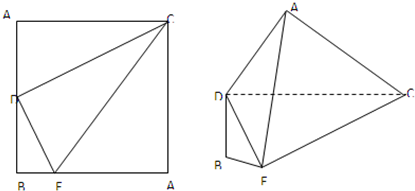 如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.
如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.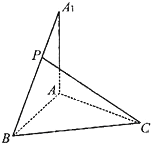 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点. 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6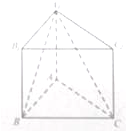 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2