考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间角
分析:(Ⅰ)法1,利用线面垂直的性质证明DE⊥面ACD,即可证明AC⊥DE;法2:建立坐标系,利用向量法进行证明.
(Ⅱ)求出平面的法向量,根据向量之间的关系即可求二面角A-DE-C的余弦值.
解答:
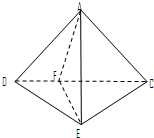
证明:(Ⅰ)法1:∵A
1,A
2重合于A,
∴AC⊥AD,AC⊥AE,故AC⊥面ADE,
∴AC⊥DE,由于A-DC-E为直二面角,
过A作AF⊥CD于F,则AF⊥面CDE
∴AF⊥DE,AC∩AF=A
∴DE⊥面ACD,
∵AC?面ACD,
∴AC⊥DE,
法2:分别以AD,AE,AC为x轴,y轴,z轴建立空间直角坐标系
D(2,0,0),E(0,2,0),C(0,0,4)
(1)∵
=(2,-2,0),
=(0,0,4),
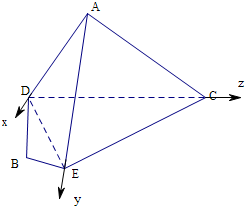
∴
•=2×0-2×0+0×4=0,
∴AC⊥DE
(Ⅱ)
=(0,-2,4),设平面DCE的法向量为
=(x,y,z),
∴由
,
令z=1,则x=y=2,即
=(2,2,1),
又AC⊥平面ADE,
∴平面ADE的法向量为
=(0,0,1),
∴二面角A-DE-C的余弦值为cosθ=
|cos<,>|=
=
=.
点评:本题考查的知识点是二面角的大小,直线与平面垂直的性质,熟练掌握线线垂直,线面垂直,面面垂直之间的转化及线面夹角的定义是解答本题的关键.

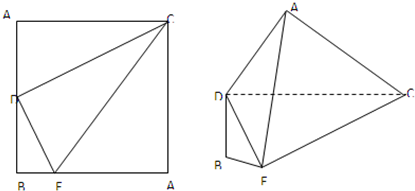 如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.
如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC. 证明:(Ⅰ)法1:∵A1,A2重合于A,
证明:(Ⅰ)法1:∵A1,A2重合于A,


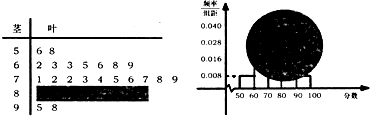 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题: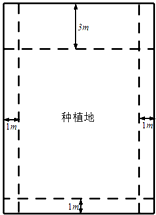 某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
某部队驻扎在青藏高原上,那里海拔高、寒冷缺氧、四季风沙、没有新鲜蔬菜,生活条件极为艰苦.但战士们不计个人得失,扎根风雪高原,以钢铁般的意志,自力更生,克服恶劣的自然环境.该部队现计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,与左、右两侧及后侧的内墙各保留1m宽的通道,与前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?