Question

已知函数f（x）=x³+ax²+bx+c的一个零点为x=1，另外两个零点分别在（0，1）和（1，+∞）内．
（1）求a+b+c；
（2）求的取值范围．

Answer 1

解：（1）根据题意，可得
∵函数f（x）=x³+ax²+bx+c的一个零点为x=1，
∴f（1）=1+a+b+c=0，即a+b+c=-1
（2）由（1），得c=-1-a-b代入f（x）解析式，得
f（x）=x³+ax²+bx-1-a-b=（x-1）（x²+x+1）+a（x+1）（x-1）+b（x-1）=（x-1）[x²+（a+1）x+1+a+b）
设g（x）=x²+（a+1）x+1+a+b，
∵f（x）的另外两个零点分别在（0，1）和（1，+∞）内
∴函数g（x）的两个零点x₁、x₂满足：0＜x₁＜1 x₂＞1，
因此，可得，
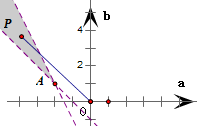
利用用线性规划知识，可得得-2＜＜-．
分析：（1）根据题意，将x=1代入f（x）解析式，即可得到a+b+c的值为0；
（2）由（1）将c=-1-a-b代入化简，可得f（x）=（x-1）[x²+（a+1）x+1+a+b）．设g（x）=x²+（a+1）x+1+a+b，由题意可得g（x）的两个零点满足0＜x₁＜1 x₂＞1，由此建立关于a、b的二元一次不等式组，在aob坐标系利用线性规划知识，即可求出的取值范围．
点评：本题给出三次多项式函数，在已知零点的分布情况下，求f（1）的值并讨论的取值范围，着重考查了多项式函数的零点分布和简单线性规划等知识，属于中档题．