Question

6．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，BC∥AD，AB⊥AD，AB=BC=$\frac{1}{3}$AD，过BC的平面交PD于M，交PA于N（N与A不重合）．
（1）求证：MN∥BC；
（2）若PM=$\frac{1}{3}$PD，求证：AC⊥BM．

Answer 1

分析 （1）根据线面平行的性质定理即可证明MN∥BC；
（2）取AE=$\frac{1}{3}$AD，根据线面垂直的性质定理证明AC⊥BM．

解答 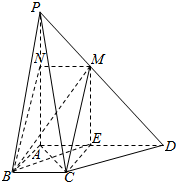证明：（1）∵BC∥AD，BC?平面PAD，AD?平面PAD，
∴BC∥平面PAD，
∵平面PAD∩平面BCMN=MN，
∴BC∥MN，即MN∥BC；
（2）取AE=$\frac{1}{3}$AD，则ME∥PA，AE=AB．
∵PA⊥底面ABCD，
∴ME⊥底面ABCD，∴ME⊥AC，
∵BC∥AD，AB⊥AD，
∴ABCE是正方形，
∴AC⊥BE，
∵ME∩BE=E，
∴AC⊥平面MBE，
∵BM?平面MBE，
∴AC⊥BM．

点评 本题主要考查线面垂直和线面平行的判定和性质，综合考查空间直线和平面的位置关系的判定，要求熟练掌握相应的判定定理和性质定理，考查学生的运算和推理能力．