练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知函数f（x）=2（x-$\frac{1}{x}$）-2ln x，则曲线y=f（x）在点（1，f（1））处的切线方程是（　　）
    A．2x+y-2=0B．2x-y-2=0C．x+y-2=0D．y=0

    分析 求出原函数的导函数，求出切点坐标，切线的斜率，然后由直线方程的点斜式得曲线y=f（x）在点（1，f（1））处的切线方程．

    解答 解：由函数f（x）=2（x-$\frac{1}{x}$）-2ln x，f（1）=0．
    得y′=2+$\frac{2}{{x}^{2}}$-$\frac{2}{x}$，
    ∴y′|x=1=2．即曲线f（x）=2（x-$\frac{1}{x}$）-2ln 在点（1，0）处的切线的斜率为：2．
    ∴曲线f（x）=2（x-$\frac{1}{x}$）-2ln 在点（1，0）处的切线方程为y-0=2×（x-1），
    整理得：2x-y-2=0．
    故选：B．

    点评 本题考查利用导数研究曲线上某点处的切线方程，曲线上过某点处的切线的斜率，就是函数在该点处的导数值，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知i是虚数单位，则复数z=$\frac{4+3i}{3-4i}$的共轭复数的虚部是（　　）
    A．-iB．iC．1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知数列{an}的前n项和S${\;}_{n}=A{q}^{n}+B（q≠0）$，则“A=-B“是“数列{an}是等比数列”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设定义在R上的连续函数f（x）满足：
    （1）对任意的实数x，都有f（-x）-f（x）=0；
    （2）对任意的实数x，都有f（x+π）+f（x）=1；
    （3）当x∈[0，π]时，0≤f（x）≤1；
    （4）当x∈（0，$\frac{π}{2}$）∪（$\frac{π}{2}$，π）时，有（x-$\frac{π}{2}$）f′（x）＞0（其中f′（x）为函数f（x）的导函数）．
    则方程f（x）=|sinx|在[-2π，2π]上的根的个数为（　　）
    A．4B．6C．8D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

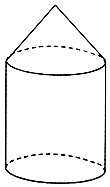    19．如图，某粮仓是由圆柱和圆锥构成（粮仓的底部位于地面上），圆柱的底面直径与高都等于h米，圆锥的高为$\frac{1}{2}$h米．
    （1）求这个粮仓的容积；
    （2）求制作这样一个粮仓的用料面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设Sn为数列{an}的前n项和，且满足${S_n}={（{-1}）^n}{a_n}-\frac{1}{2^n}$，则a2=$\frac{1}{4}$；S1+S3+S5+…+S2017=$\frac{1}{3}（\frac{1}{{2}^{2018}}-1）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知a＞0且b＞0，函数g（x）=2x，且g（a）•g（b）=2，则ab的最大值是$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

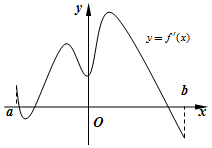    13．函数f（x）的定义域为开区间（a，b），其导函数f'（x）在（a，b）图象如图所示，则函数f（x）在开区间（a，b）内的极小值的个数是1个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1（a＞0）的离心率为2，则a等于（　　）
    A．2B．$\sqrt{3}$C．$\frac{3}{2}$D．1

    查看答案和解析>>

    同步练习册答案