Question

2．下列命题：
①常数列既是等差数列又是等比数列；
②若直线l：y=kx-$\sqrt{3}$与直线2x+3y-6=0的交点位于第一象限，则直线l的倾斜角的取值范围是（$\frac{π}{6}$，$\frac{π}{2}$）；
③若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$
④如果（a-2）x²+（a-2）x-1≤0对任意实数x总成立，则a的取值范围是[-2，2]．
其中所有正确命题的序号是②④．

Answer 1

分析 ①当常数列的项是0时，不是等比数列；
②利用数形结合求出直线l的倾斜角取值范围即可；
③当$\overrightarrow{a}$⊥$\overrightarrow{b}$时，有$\overrightarrow{a}$•$\overrightarrow{b}$=0；
④根据不等式恒成立，求出a的取值范围．

解答 解：对于①，当常数列的项是0时，它是等差数列，不是等比数列，∴①错误；
对于②，如图所示，直线l：y=kx-$\sqrt{3}$是过定点（0，-$\sqrt{3}$）的直线，
与直线2x+3y-6=0的交点位于第一象限时，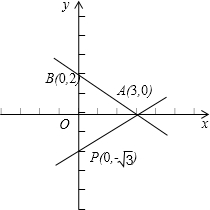
直线PA的斜率是$\frac{0+\sqrt{3}}{3-0}$=$\frac{\sqrt{3}}{3}$，对应的倾斜角为$\frac{π}{6}$，
直线PB的斜率不存在，对应的倾斜角为$\frac{π}{2}$，
∴直线l的倾斜角取值范围是（$\frac{π}{6}$，$\frac{π}{2}$），②正确；
对于③，当$\overrightarrow{a}$•$\overrightarrow{b}$=0时，$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$或$\overrightarrow{a}$⊥$\overrightarrow{b}$，∴③错误；
对于④，（a-2）x²+（a-2）x-1≤0对任意实数x总成立，
则a=2$\left\{\begin{array}{l}{a-2＜0}\\{{（a-2）}^{2}-4（a-2）•（-1）≤0}\end{array}\right.$
-2≤a≤-2
∴a的取值范围是[-2，2]，④正确．
综上，正确的命题是②④．
故答案为：②④．

点评 本题考查了等差与等比数列的应用问题，也考查了直线的斜率与倾斜角的应用问题，考查了平面向量的数量积以及不等式的恒成立问题，是基础题目．