
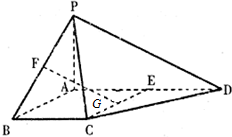
 四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,四边形ABCE为菱形,∠BAD=120°,G、F分别是线段CE,PB上的动点,且满足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,四边形ABCE为菱形,∠BAD=120°,G、F分别是线段CE,PB上的动点,且满足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$分析 (1)延长BG交CD于Q,连PQ,BE,证明FG∥PQ,即可证得FG∥平面PCD;
(2)$λ=\frac{1}{2}$,连接AC,证明CE⊥平面PAG,即可得出平面PAG⊥平面PCE.
解答 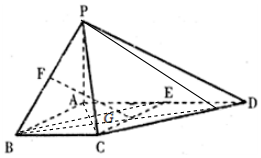 (1)证明:延长BG交CD于Q,连PQ,BE,平行四边形BEDC,则BE∥CQ,∴$\frac{CG}{GE}=\frac{OG}{GB}$.
(1)证明:延长BG交CD于Q,连PQ,BE,平行四边形BEDC,则BE∥CQ,∴$\frac{CG}{GE}=\frac{OG}{GB}$.
又∵PF:FB=CG:GE,则QG:GB=PF:FB,∴FG∥PQ.
∵FG?平面PCD,PQ?平面PCD.
∴FG∥平面PCD
(2)解:$λ=\frac{1}{2}$,连接AC,
因为∠BAD=120°的菱形,所以△ACE为等边三角形,
所以CE⊥AG,
又因为PA⊥平面ABCD,所以PA⊥CE,PA∩AG=A
所以CE⊥平面PAG,
因为CE?平面PCE,所以面PAG⊥平面PCE.
点评 熟练掌握平行线分线段成比例定理、菱形的性质、线面平行的判定定理、面面垂直的判定,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | ||
| C. | 0 | D. | 以上答案均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1,3} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | y2=6x | C. | y2=8x | D. | y2=16x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数77.5,中位数77.5.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数77.5,中位数77.5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com