
分析 (1)在等式f(m+n)+f(m-n)=2f(m)?f(n)中,令m=x0,n=0,即可求得f(0)=1,结合f(m+n)+f(m-n)=2f(m)?f(n)、f(1+m)=f(1-m)、f(x)不恒为0,且当0<x<1时,f(x)<1即可求得f(1)的值;
(2)在f(m+n)+f(m-n)=2f(m)?f(n)中,取m=0,n=x,以及有f(0)=1,可得函数f(x)为偶函数;
(3)由f(1+m)=f(1-m),并取1+m=-x,得f(-x)=f(2+x),又f(x)为偶函数,可得f(x+2)=f(x),即f(x)是以2为周期的周期函数;
在f(m+n)+f(m-n)=2f(m)?f(n)中,取$m=n=\frac{1}{3}$,取m=$\frac{2}{3}$,n=$\frac{1}{3}$得到两个关于f($\frac{2}{3}$)和f($\frac{1}{3}$)的方程组,求出f($\frac{2}{3}$)和f($\frac{1}{3}$),再由函数的周期性求得$f(\frac{1}{3})+f(\frac{2}{3})+f(\frac{3}{3})+…+f(\frac{2017}{3})$的值.
解答 (1)解:由于f(x)不恒为0,故存在x0,使f(x0)≠0,令m=x0,n=0,
则f(x0)+f(0)=2f(x0)f(0),∴f(0)=1,
令m=n=1⇒f(2)+f(0)=2f2(1),
由f(1+m)=f(1-m)并令m=1得:f(2)=f(0),
结合以上结果可得f2(1)=1,
又令$m=n=\frac{1}{2},f(1)+f(0)=2f(\frac{1}{2})?f(\frac{1}{2})<2$ (因为$f(\frac{1}{2})<1$),
∴f(1)<1,故f(1)=-1;
(2)解:f(x)为偶函数.
证明如下:
令m=0,n=x,得:f(x)+f(-x)=2f(0)f(x),以及有f(0)=1,
即有f(-x)=f(x),即有f(x)为偶函数;
(3)证明:由f(1+m)=f(1-m),并取1+m=-x,得f(-x)=f(2+x),又f(x)为偶函数,
则f(x+2)=f(x),即f(x)是以2为周期的周期函数;
令$m=n=\frac{1}{3}⇒f(\frac{2}{3})+f(0)=2{f}^{2}(\frac{1}{3})⇒f(\frac{2}{3})+1=2{f}^{2}(\frac{1}{3})$,
再令m=$\frac{2}{3}$,n=$\frac{1}{3}$⇒$f(1)+f(\frac{1}{3})=2f(\frac{2}{3})f(\frac{1}{3})$⇒$-1+f(\frac{1}{3})=2f(\frac{2}{3})f(\frac{1}{3})$.
而$f(\frac{2}{3})<1$,解得,$f(\frac{1}{3})=\frac{1}{2},f(\frac{2}{3})=-\frac{1}{2}$,
由f(1+m)=f(1-m)得,$f(\frac{1}{3})=f(\frac{5}{3}),f(\frac{2}{3})=f(\frac{4}{3})$,
∴$f(\frac{1}{3})+f(\frac{2}{3})+f(\frac{3}{3})+f(\frac{4}{3})+f(\frac{5}{3})+f(\frac{6}{3})=0$,
又由于f(x)是以2为周期的周期函数,
∴$f(\frac{1}{3})+f(\frac{2}{3})+f(\frac{3}{3})+…+f(\frac{2017}{3})=336×0+f(\frac{2017}{3})=f(\frac{1}{3})=\frac{1}{2}$.
点评 本题主要考查抽象函数的应用,利用赋值法结合函数奇偶性和周期性的定义判断函数的性质是解决本题的关键,是中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},\frac{1}{{\sqrt{e}}})∪(\frac{1}{{\sqrt{2}}},\frac{1}{{\root{3}{2}}})$ | B. | $(\frac{1}{{\sqrt{2}}},\frac{1}{{\root{3}{2}}})∪[2,+∞)$ | ||
| C. | $(\frac{1}{2},\frac{1}{{\sqrt{e}}})∪[2,+∞)$ | D. | $(\frac{1}{2},\frac{1}{{\sqrt{e}}})∪(\frac{1}{{\sqrt{2}}},\frac{1}{{\root{3}{2}}})∪[2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正△ABC两边AB,AC的中点分别为M,N,直线MN与△ABC外接圆的一个交点为P.
正△ABC两边AB,AC的中点分别为M,N,直线MN与△ABC外接圆的一个交点为P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
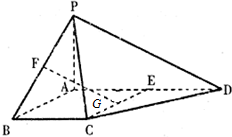 四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,四边形ABCE为菱形,∠BAD=120°,G、F分别是线段CE,PB上的动点,且满足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,四边形ABCE为菱形,∠BAD=120°,G、F分别是线段CE,PB上的动点,且满足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com