已知双曲线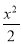
－y2＝1的左、右顶点分别为A1，A2，点P(x1，y1)，Q(x1，－y1)是双曲线上不同的两个动点．求直线A1P与A2Q交点的轨迹E的方程．
阅读快车系列答案科目：高中数学 来源：2015高考数学（理）一轮配套特训：选4-1-1相似三角形判定及性质（解析版） 题型：填空题
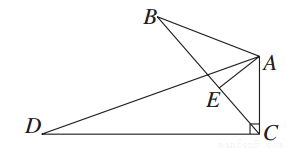
如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则BE＝________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：9-1随机抽样（解析版） 题型：填空题
某报社做了一次关于“什么是新时代的雷锋精神”的调查，在A，B，C，D四个单位回收的问卷数依次成等差数列，且共回收1000份，因报道需要，再从回收的问卷中按单位分层抽取容量为150的样本，若在B单位抽取30份，则在D单位抽取的问卷是________份．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-9圆锥曲线的综合问题（解析版） 题型：选择题
已知抛物线y2＝4x的准线与双曲线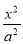
－y2＝1交于A、B两点，点F是抛物线的焦点，若△FAB为直角三角形，则该双曲线的离心率为( )
A．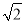
B．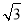
C．2 D．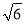
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-8曲线与方程（解析版） 题型：填空题
若动圆M与圆C1：(x＋4)2＋y2＝2外切，且与圆C2：(x－4)2＋y2＝2内切，则动圆圆心M的轨迹方程________．
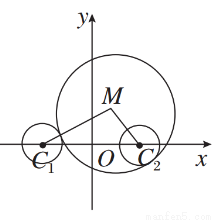
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-8曲线与方程（解析版） 题型：选择题
设F(1,0)，M点在x轴上，P点在y轴上，且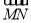
＝2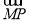
，
⊥
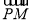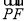，当点P在y轴上运动时，点N的轨迹方程为( )
A．y2＝2x B．y2＝4x
C．y2＝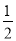
x D．y2＝
x
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-7抛物线（解析版） 题型：选择题
已知直线l1：4x－3y＋11＝0和直线l2：x＝－1，抛物线y2＝4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A．2 B．3 C．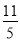
D．
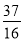
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-6双曲线（解析版） 题型：解答题
设圆C与两圆(x＋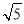
)2＋y2＝4，(x－
)2＋y2＝4中的一个内切，另一个外切．
(1)求C的圆心轨迹L的方程；
(2)已知点M(
，
)，F(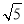
，0)，且P为L上动点，求||MP|－|FP||的最大值及此时点P的坐标．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-4直线与圆、圆与圆的位置关系（解析版） 题型：选择题
若点P(3，－1)为圆(x－2)2＋y2＝25的弦AB的中点，则直线AB的方程为( )
A．x＋y－2＝0 B．2x－y－7＝0
C．2x＋y－5＝0 D．x－y－4＝0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋y2＝1，x≠0
，A1(－
，0)，A2(
，0)，则有直线A1P的方程为y＝
(x＋
) ①，
(x－
) ②．
，即
③，则x≠0，|x|<
．
－y2＝1上，所以
－
＝1．
