
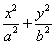 ��1(a��b��0)��������Ϊ
��1(a��b��0)��������Ϊ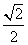 ���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(
���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(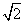 ��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D.
��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D. 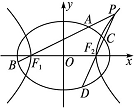
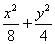 ��1.
��1.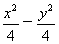 ��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)��
��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)��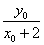 ��k2��
��k2��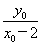 .��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.
.��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.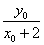 ��
��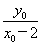 ��
��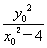 ��1����k1��k2��1.
��1����k1��k2��1.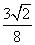 ��ʹ|AB|��|CD|����|AB|��|CD|�������
��ʹ|AB|��|CD|����|AB|��|CD|�������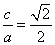 ��
�� 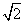 ��1)������a��2
��1)������a��2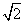 ��c��2.
��c��2.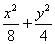 ��1.
��1.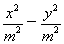 ��1(m��0)����Ϊ����˫���ߵĶ�������Բ�Ľ��㣬����m��2�����˫���ߵı�����Ϊ
��1(m��0)����Ϊ����˫���ߵĶ�������Բ�Ľ��㣬����m��2�����˫���ߵı�����Ϊ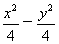 ��1.
��1.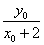 ��k2��
��k2��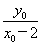 .
.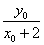 ��
��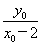 ��
��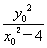 ��1����k1��k2��1.
��1����k1��k2��1.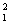 ��1)x2��8k
��1)x2��8k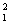 x��8k
x��8k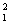 ��8��0��
��8��0��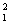 ��1��0����Ȼ����0.��Τ�ﶨ����x1��x2��
��1��0����Ȼ����0.��Τ�ﶨ����x1��x2��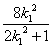 ��x1x2��
��x1x2��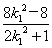 .
.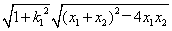
 .
.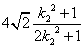 .
.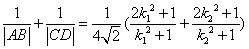 ��
��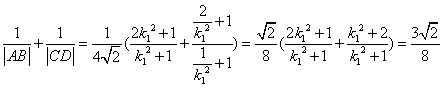 .
.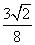 |AB|��|CD|.
|AB|��|CD|.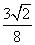 ��ʹ|AB|��|CD|����|AB|��|CD|�������
��ʹ|AB|��|CD|����|AB|��|CD|�������

 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��8 | B��11 |
| C��12 | D��10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
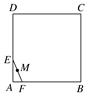
 �У�˫����������ԭ�㣬������
�У�˫����������ԭ�㣬������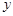 ���ϣ�һ�������߷���Ϊ
���ϣ�һ�������߷���Ϊ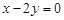 ��
��A��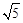 | B��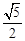 | C��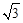 | D��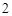 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
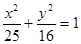 �ϵ�һ��P������Բһ������ľ���Ϊ������P����һ�������Ϊ�� ��
�ϵ�һ��P������Բһ������ľ���Ϊ������P����һ�������Ϊ�� ��| A���� | B���� | C���� | D���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
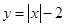 ��ͼ��������
��ͼ��������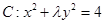 ǡ����������ͬ�Ĺ����㣬��ʵ��
ǡ����������ͬ�Ĺ����㣬��ʵ��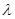 ��ȡֵ��Χ��
��ȡֵ��Χ��A��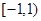 | B��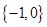 | C��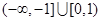 | D��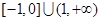 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
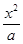 +
+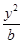 =1(
=1(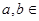 {1��2��3��4������2013})�������У�����Բ����ĺ͵��� ����������С����Բ����Ϊ .
{1��2��3��4������2013})�������У�����Բ����ĺ͵��� ����������С����Բ����Ϊ .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
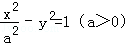 �����ĺ��㣬��PΪ˫������֧�ϵ�����һ�㣬��
�����ĺ��㣬��PΪ˫������֧�ϵ�����һ�㣬��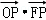 ��ȡֵ��ΧΪ
��ȡֵ��ΧΪA��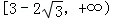 | B��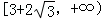 |
C��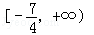 | D��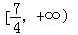 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
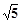 ��������e=
��������e=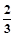 ����Բ��������ΪF1��F2����F1��ֱ�߽���Բ��A��B���㣬���ABF2�ܳ�Ϊ_____________��
����Բ��������ΪF1��F2����F1��ֱ�߽���Բ��A��B���㣬���ABF2�ܳ�Ϊ_____________���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
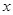 �ᣬ��ʵ�᳤Ϊ2��������
�ᣬ��ʵ�᳤Ϊ2��������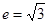 , L�ǹ�����
, L�ǹ�����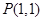 ��ֱ��.
��ֱ��.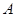 ,
,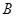 ���㣬���߶�
���㣬���߶�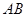 ǡ���Ե�
ǡ���Ե�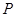 Ϊ�е㣬�����ڣ����ֱ��L�ķ��̣������棬˵������.
Ϊ�е㣬�����ڣ����ֱ��L�ķ��̣������棬˵������.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com