
| PF |
| OD |
| PO |
| 7 |
| 2 |
| ac-b2 |
| b |
| u |
| 2 |
| v |
| 2 |
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
| PF |
| OD |
| PO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| ac-b2 |
| b |
| u |
| 2 |
| a-c |
| 2 |
| v |
| 2 |
| b2-ac |
| 2b |
| a-c |
| 2 |
| b2-ac |
| 2b |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
| PF |
| OD |
| PO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| x2 |
| 8 |
| y2 |
| 4 |


科目:高中数学 来源: 题型:
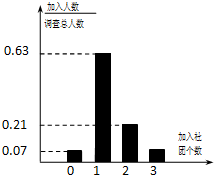 为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.
为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| cosx-sinx |
| sinx-cosx |
| 1-2sinxcosx |
| cos2x-sin2x |
| 2 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com