
分析 由题意根据余弦函数的图象的对称性求得φ的值,可得函数的解析式,再利用诱导公式求得f(x+$\frac{π}{3}$)的解析式,结合正弦函数的奇偶性和单调性,求得函数y=f(x+$\frac{π}{3}$)的单调减区间.
解答 解:∵f(x)=cos(2x+φ)的图象关于点($\frac{4π}{3}$,0)成中心对称,且-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴2•$\frac{4π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,即φ=-$\frac{π}{6}$,f(x)=cos(2x-$\frac{π}{6}$).
则函数y=f(x+$\frac{π}{3}$)=cos[2(x+$\frac{π}{3}$)-$\frac{π}{6}$]=cos(2x+$\frac{π}{2}$)=-sin2x,为奇函数.
再令2kπ+$\frac{π}{2}$≤2x≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{4}$≤x≤kπ+$\frac{3π}{4}$,k∈Z,
可得函数y=f(x+$\frac{π}{3}$)的单调减区间为[kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$],k∈Z,
故答案为:奇;[kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$],k∈Z.
点评 本题主要考查余弦函数的图象的对称性,诱导公式,正弦函数的奇偶性和单调性,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
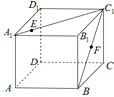 在正方体ABCD-A1B1C1D1中,F为线段BC1的中点,E为直线A1C1上的动点,则下列结论中正确的为( )
在正方体ABCD-A1B1C1D1中,F为线段BC1的中点,E为直线A1C1上的动点,则下列结论中正确的为( )| A. | 存在点E使EF∥BD1 | B. | 不存在点E使EF⊥平面AB1C1D | ||
| C. | 三棱锥B1-ACE的体积为定值 | D. | EF与AD1不可能垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{36}$] | B. | (0,$\frac{1}{9}$] | C. | (0,$\frac{1}{6}$] | D. | (0,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从甲、乙两个班级各抽取5名学生参加英语口语竞赛,他们的成绩的茎叶图如图:其中甲班学生的平均成绩是85,乙班学生成绩的中位数是84,则x+y的值为( )
从甲、乙两个班级各抽取5名学生参加英语口语竞赛,他们的成绩的茎叶图如图:其中甲班学生的平均成绩是85,乙班学生成绩的中位数是84,则x+y的值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 240 | C. | 500 | D. | 512 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 导函数为$f'(x)=3cos(2x-\frac{π}{3})$ | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{2}$对称 | |
| C. | 函数f(x)在区间$(-\frac{π}{12},\frac{5π}{12})$上是增函数 | |
| D. | 函数f(x)的图象可由函数y=3sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com