练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，AE切⊙D于点E，AC=CD=DB=10，则线段AE的长为（ ）

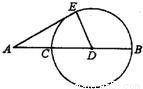
    A.10 B.16 C.10 D.18

     

    C

    【解析】

    试题分析：根据切线的性质得∠AED=90°，然后利用已知条件根据勾股定理即可求出AE．

    【解析】
    ∵AE切⊙D于点E，

    ∴∠AED=90°，

    ∵AC=CD=DB=10，

    ∴AD=20，DE=10，

    ∴AE===10 ．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷（解析版） 题型：

    在z轴上与点A（﹣4，1，7）和点B（3，5，﹣2）等距离的点C的坐标为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量（解析版） 题型：填空题

    已知矩阵M=的一个特征值为﹣1，则其另一个特征值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：填空题

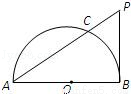
    （2014•清远一模）如图，O是半圆的圆心，直径AB=2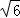，PB是圆的一条切线，割线PA与半圆交于点C，AC=4，则PB= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

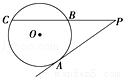
    如图，PA是⊙O的切线，A为切点，PC是⊙O的割线，且PB=BC，则等于（ ）

    A.2 B. C.1 D.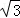

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为（ ）

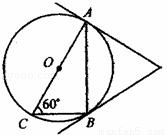
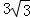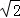    A. B. C.3 D.2

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习（解析版） 题型：选择题

    （2010•崇文区一模）如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B．如果∠APB=60°，PA=8，那么点P与O间的距离是（ ）

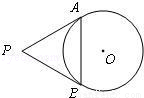
    A.16 B.20 C.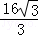 D.

     

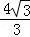
    查看答案和解析>>

    科目：高中数学 来源：[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理（解析版） 题型：选择题

    如图，锐角三角形ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则△ADE与△ABC的面积之比为（ ）

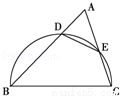
    A.cosA B.sinA C.sin2A D.cos2A

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷（解析版） 题型：选择题

    若，则复数（cosθ+sinθ）+（sinθ﹣cosθ）i在复平面内所对应的点在（ ）

    A.第一象限 B.第二象限 C.第三象限 D.第四象限

     

    查看答案和解析>>

    同步练习册答案