
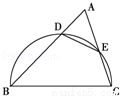
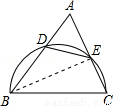
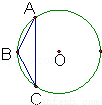
如图,锐角三角形ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则△ADE与△ABC的面积之比为( )
A.cosA B.sinA C.sin2A D.cos2A
D
【解析】
试题分析:连接BE.构建直角△ABE,通过解该直角三角形求得cosA= ;然后通过相似三角形△AED∽△ABC的对应边的比成比例知
;然后通过相似三角形△AED∽△ABC的对应边的比成比例知 =
=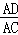 ;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.
;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.
【解析】
如图,连接BE.
∵BC为半圆的直径,
∴∠BEC=∠AEB=90°.
∴在直角△ABE中,cosA= ,
,
∵点D、B、C、E四点共圆,
∴∠ABC+∠DEC=180°.
∵∠DEC+∠AED=180°,
∴∠ABC=∠AED.
又∵∠A=∠A,
∴△AED∽△ABC,
∴ =
=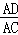 .
.
∵S△ADE=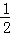 AE•AD•sinA,S△ABC=
AE•AD•sinA,S△ABC=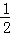 AB•AC•sinA,
AB•AC•sinA,
∴S△ADE:S△ABC=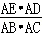 =
= =cos2A.
=cos2A.
故选:D.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
在空间,下列命题中正确的是( )
A.对边相等的四边形一定是平面图形
B.有一组对边平行的四边形一定是平面图形
C.四边相等的四边形一定是平面图形
D.有一组对角相等的四边形一定是平面图形
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为( )
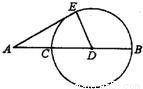
A.10 B.16 C.10 D.18
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2013•珠海一模)(几何证明选讲选做题)
如图所示,等腰三角形ABC的底边AC长0为6,其外接圆的半径长为5,则三角形ABC的面积是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
下列四边形中,四个顶点一定在同一个圆上的是( )
A.平行四边行 B.菱形 C.矩形 D.直角梯形
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
直线x+3y﹣7=0与kx﹣y﹣2=0与两坐标轴围成的四边形内接于一个圆,则实数k=( )
A.﹣3 B.3 C.﹣6 D.6
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
在复平面内,复数z=sin2+icos2对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
某商品一件的成本为30元,在某段时间内,若以每件x元出售,可卖出(200﹣x)件,当每件商品的定价为 元时,利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com