
分析 可先分离常数得到y=$2-\frac{4(x-2)}{{x}^{2}-2x+4}$,分子上是x-2,可考虑能否让分母也出现x-2:x2-2x+4=(x-2)2+2(x-2)+4,从而分子分母同时除以x-2便可得到$y=2-\frac{4}{(x-2)+\frac{4}{x-2}+2}$,从而可根据基本不等式得到$(x-2)+\frac{4}{x-2}$的范围,进一步得到$\frac{1}{(x-2)+\frac{4}{x-2}+2}$的范围,从而可得出y的范围,即得出原函数的值域.
解答 解:将原函数变成:$y=\frac{2({x}^{2}-2x+4)-4x+8}{{x}^{2}-2x+4}=2+\frac{-4x+8}{{x}^{2}-2x+4}$=$2-\frac{4}{\frac{(x-2)^{2}+2(x-2)+4}{x-2}}=2-\frac{4}{(x-2)+\frac{4}{x-2}+2}$;
∵x>2;
∴x-2>0;
∴$(x-2)+\frac{4}{x-2}≥4$,x=4时取“=”;
∴$0<\frac{1}{(x-2)+\frac{4}{x-2}+2}≤\frac{1}{6}$;
∴$\frac{4}{3}≤y<2$;
∴原函数的值域为$[\frac{4}{3},2)$.
点评 考查函数值域的概念,分离常数法的运用,凑出基本不等式$x+\frac{a}{x}$的形式,然后应用基本不等式求值域的方法,注意判断等号能否取到,以及不等式的性质.


科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
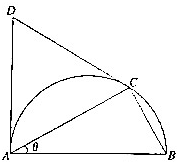 如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),
如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com