Question

13．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+4x，x≤0\\ xlnx，x＞0\end{array}\right.$，g（x）=kx-1，若方程f（x）-g（x）=0在x∈（-2，2）有三个实根，则实数k的取值范围为（　　）

• A． $（1，ln2\sqrt{e}）$
• B． $（ln2\sqrt{e}，\frac{3}{2}）$
• C． $（\frac{3}{2}，2）$
• D． $（1，ln2\sqrt{e}）∪（\frac{3}{2}，2）$

Answer 1

分析 显然x=0时，原方程无解；可化为k=$\frac{f（x）+1}{x}$，讨论x＜0，x＞0时，通过导数或基本不等式可得最值和单调区间，作出φ（x）在x∈（-2，2）图象，和直线y=k，观察可得三个交点的情况，即可得到所求k的范围．

解答 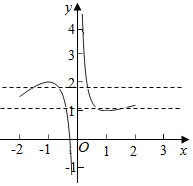解：显然，x=0不是方程f（x）-g（x）=0的根，
则f（x）-g（x）=0，即为k=$\frac{f（x）+1}{x}$，
可设$k=φ（x）=\left\{\begin{array}{l}x+\frac{1}{x}+4，x＜0\\ \frac{1}{x}+lnx，x＞0\end{array}\right.$，
由x＜0，可得φ（x）=x+$\frac{1}{x}$+4≤-2$\sqrt{（-x）•\frac{1}{-x}}$+4=2，
即有φ（x）在x＜0时，有最大值φ（-1）=2；
当x＞0时，φ（x）=$\frac{1}{x}$+lnx的导数为φ′（x）=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-1}{{x}^{2}}$，
在x＞1时，φ′（x）＞0，φ（x）递增；在0＜x＜1时，φ′（x）＜0，φ（x）递减．
可得x=1处取得最小值1．
作出φ（x）在x∈（-2，2）图象得
在1＜k＜ln2+$\frac{1}{2}$或-2-$\frac{1}{2}$+4＜k＜2时，直线y=k和y=φ（x）的图象均有三个交点．
则k的取值范围是（1，ln2$\sqrt{e}$）∪（$\frac{3}{2}$，2）．
故选：D．

点评 本题考查函数方程的转化思想的运用，考查导数的运用：求单调性和最值，考查数形结合的思想方法，考查运算能力，属于中档题．