
����Ŀ��ijʡ2016�������ѧѧҵˮƽ���Ե�ԭʼ�ɼ����ðٷ��ƣ������ɼ�ʹ�õȼ��ƣ����ȼ����ֱ����£�85�ּ����ϣ���ΪA�ȣ�������[70��85���ڣ���ΪB�ȣ�������[60��70���ڣ���ΪC�ȣ�60�����£���ΪD�ȣ�ͬʱ�϶�A��B��CΪ�ϸ�DΪ���ϸ���֪ijѧУѧ����ԭʼ�ɼ����ֲ���[50��100]�ڣ�Ϊ���˽��Уѧ���ijɼ�����ȡ��50��ѧ����ԭʼ�ɼ���Ϊ��������ͳ�ƣ�����[50��60����[60��70����[70��80����[80��90����[90��100]�ķ�����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
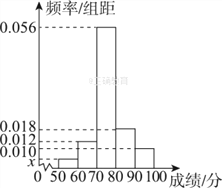
��������ͼ��x��ֵ���������������ݹ��Ƹ�Уѧ��ѧҵˮƽ���Եĺϸ��ʣ�
��������ѡȡ�������У���70�����µ�ѧ���������ȡ3��ѧ�����е��У���X��ʾ����ȡ��3��ѧ���гɼ�ΪD�ȼ������������������X�ķֲ��к���ѧ������
���𰸡����� 0.96 ���ֲ��м����� ![]()
���������������������������Ƶ�ʷֲ�ֱ��ͼ�����ʵ�xֵ���ҳ�60�����ϵĸ�����͵ý��
��������ȷ��C D�ȼ������������ó����ηֲ�![]() �ó����
���
���������
�����������֪��10x��0.012��10��0.056��10��0.018��10��0.010��10��1��
��x��0.004��
��ϸ���Ϊ1��10��0.004��0.96��
����������C�ȼ���ѧ������Ϊ0.012��10��50��6��
��D�ȼ���ѧ������Ϊ0.004��10��50��2��
�������ȡ3���У��ɼ�ΪD�ȼ�������X�Ŀ���ȡֵΪ0��1��2��
��![]() ��
�� ![]() ��
�� ![]() ��
��
��X�ķֲ���Ϊ
x | 0 | 1 | 2 |
P |
|
|
|
��ѧ����![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() = x��ex��
= x��ex�� ![]() ��
�� ![]() �����������
�����������![]() ������
������![]() ��������ʵ��k��ȡֵ��Χ��
��������ʵ��k��ȡֵ��Χ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵxOy�У�����C1�IJ�������Ϊ![]() ��tΪ����������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�����C2��
��tΪ����������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�����C2�� ![]() ��
��
����������C1��C2��ֱ�����귽�̣����ֱ�ָ�����������ͣ�
�������жϣ�����C1��C2�Ƿ��й����㣿����У�˵��������ĸ��������û�У���˵�����ɣ�
������![]() ������C1������һ�㣬��ֱ��д��a + 2b��ȡֵ��Χ��
������C1������һ�㣬��ֱ��д��a + 2b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲC�IJ�������Ϊ![]() ����Ϊ��������ֱ��l�IJ�������Ϊ
����Ϊ��������ֱ��l�IJ�������Ϊ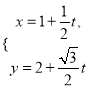 ��tΪ��������
��t��������
������д����ԲC����ͨ���̺�ֱ��l����б�ǣ�
����������P��1��2������ֱ��l����ԲC�ཻ��A��B���㣬��|PA|��|PB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵��顰��һ��С���ٳ���ѡ����ˮ�ĵط����Ƿ����Ա��йأ��ִӸ��С���һ�������ÿ��������ȡ500�˽��е��飬�õ�����2��2������������λ���ˣ�
ѡ����ˮ�ĵط��� | ��ѡ����ˮ�ĵط��� | �ϼ� | |
�� | 90 | 110 | 200 |
Ů | 210 | 90 | 300 |
�ϼ� | 300 | 200 | 500 |
�������ݴ��������ж��İ�����Ϊѡ����ˮ�ĵط������Ա��йأ�
���������������и��¼���Ƶ����Ϊ���ʹ���ȫ�С���һ�����г����ÿ�������ִӸ��е�ȫ������ÿͣ������ڶࣩ�������ȡ3�ˣ���3����ѡ����ˮ�ĵط���������Ϊ�������X�����������X����ѧ�����ͷ��
���ٽ�ֵ�����ο���ʽ��
P��K2��k0�� | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
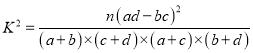 ��n��a��b��c��d��
��n��a��b��c��d��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1����֤��f��x���ڣ�0��+�ޣ����ǵ�������������
��2����f��x���� ![]() �ϵ�ֵ����
�ϵ�ֵ���� ![]() ����a��ֵ��
����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ��sin����+![]() ��=
��=![]() ������C�IJ�������Ϊ
������C�IJ�������Ϊ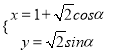 ����Ϊ��������
������������
��1����ֱ��l����ͨ���̣�
��2����P������C�ϵĶ��㣬���P��ֱ��l�������뼰��P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com