Question

【题目】已知集合M={x|x2﹣3x≤10}，N={x|a﹣1≤x≤2a+1}．
（1）若a=2，求（RM）∪N；
（2）若M∪N=M，求实数a的取值范围．

Answer 1

【答案】
（1）解：M={x|x2﹣3x≤10}={x|﹣2≤x≤5}，

若a=2，则N={x|1≤x≤3}．

则RM={x|x＞5或x＜﹣2}，

则（RM）∪N={x||x＞5或x＜﹣2或1≤x≤3}

（2）解：若M∪N=M，则NM，

若a﹣1＞2a+1，即a＜﹣2，此时N是空集，满足条件．

若a≥﹣2，则N不是空集，则满足 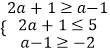，得 ，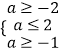

即﹣1≤a≤2，

综上a＜﹣1或﹣1≤a≤2

【解析】（1）求出集合的等价条件，利用集合的基本运算进行求解即可．（2）根据条件M∪N=M，得NM，利用集合关系进行求解即可．
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案，需要熟知求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法．