
ЁОЬтФПЁП
ЮЊСЫБЃЛЄЛЗОГЃЌЗЂеЙЕЭЬМОМУЃЌФГЕЅЮЛдкеўИЎВПУХЕФжЇГжЯТЃЌНјааММЪѕЙЅЙиЃЌВЩгУСЫаТЙЄвеЃЌаТЩЯСЫАбЖўбѕЛЏЬМзЊЛЏЮЊвЛжжПЩРћгУЕФЛЏЙЄВњЦЗЕФЯюФП.ОВтЫуЃЌдТДІРэГЩБО![]() ЃЈдЊЃЉгыдТДІРэСП
ЃЈдЊЃЉгыдТДІРэСП![]() ЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕПЩвдНќЫЦЕФБэЪОЮЊЃК
ЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕПЩвдНќЫЦЕФБэЪОЮЊЃК ЃЌЧвУПДІРэвЛЖжЖўбѕЛЏЬМПЩЕУЕНФмРћгУЕФЛЏЙЄВњЦЗМлжЕЮЊ200дЊЃЌШєИУЯюФПВЛЛёРћЃЌеўИЎНЋВЙЬљ.
ЃЌЧвУПДІРэвЛЖжЖўбѕЛЏЬМПЩЕУЕНФмРћгУЕФЛЏЙЄВњЦЗМлжЕЮЊ200дЊЃЌШєИУЯюФПВЛЛёРћЃЌеўИЎНЋВЙЬљ.
ЃЈIЃЉЕБ![]() ЪБЃЌХаЖЯИУЯюФПФмЗёЛёРћЃПШчЙћЛёРћЃЌЧѓГізюДѓРћШѓЃЛШчЙћВЛЛёРћЃЌдђеўИЎУПдТжСЩйашвЊВЙЬљЖрЩйдЊВХФмЪЙИУЯюФПВЛПїЫ№ЃЛ
ЪБЃЌХаЖЯИУЯюФПФмЗёЛёРћЃПШчЙћЛёРћЃЌЧѓГізюДѓРћШѓЃЛШчЙћВЛЛёРћЃЌдђеўИЎУПдТжСЩйашвЊВЙЬљЖрЩйдЊВХФмЪЙИУЯюФПВЛПїЫ№ЃЛ
ЃЈIIЃЉИУЯюФПУПдТДІРэСПЮЊЖрЩйЖжЪБЃЌВХФмЪЙУПЖжЕФЦНОљДІРэГЩБОзюЕЭЃП
ЁОД№АИЁПЃЈIЃЉашВЙЬљ![]() ЃЛЃЈIIЃЉ
ЃЛЃЈIIЃЉ![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈIЃЉЕБ![]() ЪБЃЌЛёРћЪЧ
ЪБЃЌЛёРћЪЧ![]() ЃЌЗбгУЪЧ
ЃЌЗбгУЪЧ![]() ЃЌСНепВюЪЧЖўДЮКЏЪ§ЃЌгУХфЗНЗЈПЩжЊИУЯюФПВЛЛсЛёРћЃЛЃЈIIЃЉЦНОљДІРэГЩБОМД
ЃЌСНепВюЪЧЖўДЮКЏЪ§ЃЌгУХфЗНЗЈПЩжЊИУЯюФПВЛЛсЛёРћЃЛЃЈIIЃЉЦНОљДІРэГЩБОМД![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЫљвдЕБ
ЃЌЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюаЁжЕ
ШЁЕУзюаЁжЕ![]() . ЕБ
. ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБУПдТДІРэСПЮЊ
ЃЌЕБУПдТДІРэСПЮЊ![]() ЖжЪБЃЌВХФмЪЙУПЖжЕФЦНОљДІРэГЩБОзюЕЭ.
ЖжЪБЃЌВХФмЪЙУПЖжЕФЦНОљДІРэГЩБОзюЕЭ.
ЪдЬтНтЮіЃК
ЃЈIЃЉЕБ![]() ЪБЃЌЩшИУЯюФПЛёРћЮЊ
ЪБЃЌЩшИУЯюФПЛёРћЮЊ![]() ЃЌдђ
ЃЌдђ
![]()
![]()
ЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌвђДЫЃЌИУЯюФПВЛЛсЛёРћЃЌ
ЃЌвђДЫЃЌИУЯюФПВЛЛсЛёРћЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕ
ШЁЕУзюДѓжЕ![]() ЃЌ
ЃЌ
ЫљвдеўИЎУПдТжСЩйашвЊВЙЬљ5000дЊВХФмЪЙИУЯюФПВЛПїЫ№
ЃЈ2ЃЉгЩЬтвтПЩжЊЃЌЪГЦЗВадќЕФУПЖжЦНОљДІРэГЩБОЮЊЃК
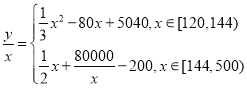 ЃЌ
ЃЌ
Ђй ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЫљвдЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюаЁжЕ240. 9Зж
ШЁЕУзюаЁжЕ240. 9Зж
Ђк ЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЌ
ЃЌ
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюаЁжЕ200ЃЌвђЮЊ200<400ЃЌЫљвдЕБУПдТДІРэСПЮЊ400ЖжЪБЃЌВХФмЪЙУПЖжЕФЦНОљДІРэГЩБОзюЕЭ.
ШЁЕУзюаЁжЕ200ЃЌвђЮЊ200<400ЃЌЫљвдЕБУПдТДІРэСПЮЊ400ЖжЪБЃЌВХФмЪЙУПЖжЕФЦНОљДІРэГЩБОзюЕЭ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНДЌЪЛЯђвЛИіВЛФмЭЌЪБЭЃВДСНЫвДЌЕФТыЭЗЃЌЫќУЧдквЛЬьЖўЪЎЫФаЁЪБФкЕНДяИУТыЭЗЕФЪБПЬЪЧЕШПЩФмЕФЃЎШчЙћМзДЌЭЃВДЪБМфЮЊ1аЁЪБЃЌввДЌЭЃВДЪБМфЮЊ2аЁЪБЃЌЧѓЫќУЧжаЕФШЮвтвЛЫвЖМВЛашвЊЕШД§ТыЭЗПеГіЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНЬх ![]() ЕФРтГЄЮЊ3ЃЌMЃЌNЗжБ№ЪЧРт
ЕФРтГЄЮЊ3ЃЌMЃЌNЗжБ№ЪЧРт ![]() ЁЂ
ЁЂ ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв ![]() .
.
ЃЈ1ЃЉжЄУїЃК ![]() ЫФЕуЙВУцЃЛ
ЫФЕуЙВУцЃЛ
ЃЈ2ЃЉЧѓМИКЮЬх ![]() ЕФЬхЛ§.
ЕФЬхЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§РтзЖ ![]() ЃЌЕзУц
ЃЌЕзУц ![]() ЪЧвд
ЪЧвд ![]() ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЖўУцНЧ
ЃЌЖўУцНЧ ![]() ЕФДѓаЁЮЊ
ЕФДѓаЁЮЊ ![]() .
.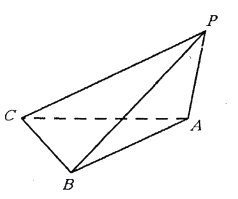
ЃЈ1ЃЉЧѓжБЯп ![]() гыЦНУц
гыЦНУц ![]() ЫљГЩНЧЕФДѓаЁЃЛ
ЫљГЩНЧЕФДѓаЁЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ ![]() ЕФе§ЧажЕ.
ЕФе§ЧажЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDКЭОиаЮACEFЫљдкЦНУцЯрЛЅДЙжБЃЌAB= ![]() ЃЌAF=1ЃЌGЮЊЯпЖЮADЩЯЕФШЮвтвЛЕуЃЎ
ЃЌAF=1ЃЌGЮЊЯпЖЮADЩЯЕФШЮвтвЛЕуЃЎ 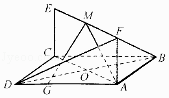
ЃЈ1ЃЉШєMЪЧЯпЖЮEFЕФжаЕуЃЌжЄУїЃКЦНУцAMGЁЭЦНУцBDFЃЛ
ЃЈ2ЃЉШєNЮЊЯпЖЮEFЩЯШЮвтвЛЕуЃЌЩшжБЯпANгыЦНУцABFЃЌЦНУцBDFЫљГЩНЧЗжБ№ЪЧІСЃЌІТЃЌЧѓ ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ ![]() ,УќЬт
,УќЬт ![]() ЃЌУќЬт
ЃЌУќЬт ![]() .
.
ЃЈ1ЃЉШє ![]() ЮЊецУќЬтЃЌЧѓЪЕЪ§
ЮЊецУќЬтЃЌЧѓЪЕЪ§ ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєУќЬт ![]() ЪЧМйУќЬт, УќЬт
ЪЧМйУќЬт, УќЬт ![]() ЪЧецУќЬт,ЧѓЪЕЪ§
ЪЧецУќЬт,ЧѓЪЕЪ§ ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкАыОЖЮЊRЕФдВФкЃЌзїФкНгЕШбќЁїABCЃЌЕБЕзБпЩЯИпhЁЪЃЈ0ЃЌt]ЪБЃЌЁїABCЕФУцЛ§ШЁЕУзюДѓжЕ ![]() ЃЌдђtЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЃЌдђtЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃДгВЮМгИпвЛФъМЖЦкжаПМЪдЕФбЇЩњжаЫцЛњГщГі60УћбЇЩњЃЌНЋЦфЮяРэГЩМЈ(ОљЮЊећЪ§)ЗжГЩСљЖЮ[40ЃЌ50)ЃЌ[50ЃЌ60)ЃЌЁЃЌ[90ЃЌ100]КѓЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌЙлВьЭМаЮЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
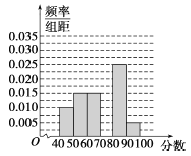
(1)ЧѓЗжЪ§дк[70ЃЌ80)ФкЕФЦЕТЪЃЌВЂВЙШЋетИіЦЕТЪЗжВМжБЗНЭМЃЛ
(2)ЭГМЦЗНЗЈжаЃЌЭЌвЛзщЪ§ОнГЃгУИУзщЧјМфЕФжаЕужЕзїЮЊДњБэЃЌОнДЫЙРМЦБОДЮПМЪджаЕФЦНОљЗжЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=|2xЉa|+|xЉ1|ЃЌaЁЪRЃЎ
ЃЈЂёЃЉШєВЛЕШЪНfЃЈxЃЉЁн2Љ|xЉ1|КуГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉЕБa=1ЪБЃЌжБЯпy=mгыКЏЪ§fЃЈxЃЉЕФЭМЯѓЮЇГЩШ§НЧаЮЃЌЧѓmЕФзюДѓжЕМАДЫЪБЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com