
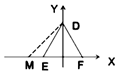
 如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )
如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )| A. | 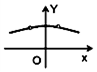 | B. | 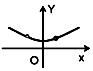 | C. | 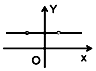 | D. |  |
分析 设△DEM的外接圆半径为R1,△DMF的外接圆半径为R2,根据正弦定理可得R1=R2,即可:f(x)=1,图象得以判断.
解答 解:设△DEM的外接圆半径为R1,△DMF的外接圆半径为R2,
则由题意,$\frac{π{R}_{1}^{2}}{π{R}_{2}^{2}}$=f(x),
点M在直线EF上从左到右运动(点M不与E、F重合),
对于M的每一个位置,由正弦定理可得:R1=$\frac{1}{2}•\frac{DE}{sin∠DME}$,R2=$\frac{1}{2}$•$\frac{DF}{sin∠DMF}$,
又DE=DF,sin∠DME=sin∠DMF,
可得:R1=R2,
可得:f(x)=1,
故选:C.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了分类讨论思想和转化思想的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
 已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.
已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2:1 | B. | 2:$\sqrt{3}$:1 | C. | 1:2:3 | D. | 1:$\sqrt{3}$:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
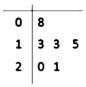 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )| A. | 中位数为14 | B. | 众数为13 | C. | 平均数为15 | D. | 方差为19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 无所谓 | 反对 | |
| 高一年级 | 18 | x | 2 |
| 高二年级 | 10 | 6 | y |
| 高一年级 | 高二年级 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com