
 已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.
已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$. 分析 设F为双曲线的左焦点,且为(-c,0),左顶点A(-a,0),设|OP|=h,则tanα=tan(∠FPO-∠APO),运用两角差的正切公式,结合基本不等式,得到e的不等式解得e即可,再由同角公式化简即可得到.
解答 解:F为双曲线的左焦点,且为(-c,0),左顶点A(-a,0),
设|OP|=h,
则tanα=tan(∠FPO-∠APO)=$\frac{tan∠FPO-tan∠APO}{1+tan∠FPOtan∠APO}$
=$\frac{\frac{c}{h}-\frac{a}{h}}{1+\frac{ac}{{h}^{2}}}$=$\frac{c-a}{h+\frac{ac}{h}}$,
由于h+$\frac{ac}{h}$≥2$\sqrt{ac}$,当且仅当h=$\sqrt{ac}$时,取等号.
即有tanα≤$\frac{c-a}{2\sqrt{ca}}$,
即2tanα≤$\sqrt{\frac{c}{a}}$-$\sqrt{\frac{a}{c}}$,
即有2tanα≤$\sqrt{e}$-$\sqrt{\frac{1}{e}}$,即e-2$\sqrt{e}$tanα-1≥0,
即$\sqrt{e}$≥tanα+$\sqrt{1+ta{n}^{2}α}$,
即有e≥($\frac{1+sinα}{cosα}$)2=$\frac{(1+sinα)^{2}}{co{s}^{2}α}$=$\frac{(1+sinα)^{2}}{1-si{n}^{2}α}$
=$\frac{1+sinα}{1-sinα}$.
当且仅当h=$\sqrt{ac}$时,e的最小值为$\frac{1+sinα}{1-sinα}$.
故答案为:$\frac{1+sinα}{1-sinα}$.
点评 本题考查双曲线的方程和性质,考查基本不等式的运用,运用两角差的正切公式是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{6}{5}$ | B. | $-\frac{7}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=logx2+1,x>0且x≠1 | B. | y=log2x+1,x>0 | ||
| C. | y=log2x-1,x>0 | D. | y=log2(x-1),x>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
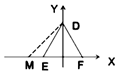 如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )
如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )| A. | 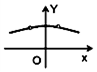 | B. | 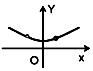 | C. | 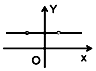 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com