
| A. | $-\frac{6}{5}$ | B. | $-\frac{7}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
分析 由已知利用两角和的正切函数公式,特殊角的三角函数值可求tanθ,进而利用同角三角函数基本关系式化简所求即可得解.
解答 解:∵$tan({θ+\frac{π}{4}})=-3$,
∴$\frac{tanθ+1}{1-tanθ}$=-3,解得:tanθ=2,
∴2sin2θ-cos2θ=$\frac{2si{n}^{2}θ-co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{2ta{n}^{2}θ-1}{ta{n}^{2}θ+1}$=$\frac{7}{5}$.
故选:D.
点评 本题主要考查了两角和的正切函数公式,特殊角的三角函数值,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | +∞ | B. | a | C. | -a | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.
已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为$\frac{1+sinα}{1-sinα}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,1),$4\sqrt{5}$ | B. | (2,1),$4\sqrt{5}$ | C. | (-3,1),$4\sqrt{3}$ | D. | (2,-1),3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
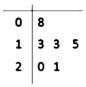 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )| A. | 中位数为14 | B. | 众数为13 | C. | 平均数为15 | D. | 方差为19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com