Question

如图所示，终边落在直线y=x上的角的集合为 ．

 

 

Answer 1

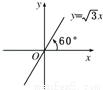
{α|α=60°+n•180°，n∈Z}．

【解析】

试题分析：由直线方程求出直线的倾斜角，再分别写出终边落在直线向上和向下方向上的角的集合，由集合的并集运算求出终边落在直线y=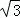x上的角的集合．

【解析】
∵直线y=x的斜率为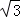，则倾斜角为60°，

∴终边落在射线y=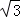x（x≥0）上的角的集合是S1={α|α=60°+k•360°，k∈Z}，

终边落在射线y=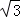x（x≤0）上的角的集合是S2={α|α=240°+k•360°，k∈Z}，

∴终边落在直线y=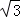x上的角的集合是：

S={α|α=60°+k•360°，k∈Z}∪{α|α=240°+k•360°，k∈Z}

={α|α=60°+2k•180°，k∈Z}∪{α|α=60°+（2k+1）•180°，k∈Z}

={α|α=60°+n•180°，n∈Z}．

故答案为：{α|α=60°+n•180°，n∈Z}．