
【题目】
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
【答案】(Ⅰ)证明见解析.
(Ⅱ)见解析.
(Ⅲ)![]()
【解析】
(Ⅰ)选择反证法来证明,假设存在推出矛盾.
(Ⅱ)用数列![]() 构造一个新数列,我们写出新数列的第
构造一个新数列,我们写出新数列的第![]() 项和第
项和第![]() 项之间的关系,发现
项之间的关系,发现![]() 的取值影响数列的性质,所以要对
的取值影响数列的性质,所以要对![]() 进行讨论.
进行讨论.
(Ⅲ)根据前面的运算写出数列的前![]() 项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意
项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意![]() 的奇偶情况要分类讨论.
的奇偶情况要分类讨论.
解:(Ⅰ)证明:假设存在一个实数![]() ,使
,使![]() 是等比数列,则有
是等比数列,则有![]() ,即
,即![]() ,矛盾.
,矛盾.
所以![]() 不是等比数列.
不是等比数列.
(Ⅱ)解:因为![]()
![]()
又![]() ,所以
,所以
当![]() ,
,![]() ,此时
,此时![]() 不是等比数列:
不是等比数列:
当![]() 时,
时,![]() ,由上可知
,由上可知![]() ,
,
![]()
![]() .
.
故当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当![]() ,
,![]() ,
,![]() ,不满足题目要求.
,不满足题目要求.
![]() ,故知
,故知![]() ,于是可得
,于是可得
![]() ,
,
要使![]() 对任意正整数
对任意正整数![]() 成立,
成立,
即![]()
得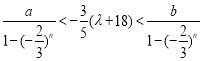
![]() ①
①
当![]() 为正奇数时,
为正奇数时,![]() ;当
;当![]() 为正偶数时,
为正偶数时,![]() ,
,
![]() 的最大值为
的最大值为![]() (1)
(1)![]() ,
,![]() 的最小值为
的最小值为![]() (2)
(2)![]() ,.
,.
于是,由①式得![]() .
.
当![]() 时,由
时,由![]() ,不存在实数满足题目要求;
,不存在实数满足题目要求;
当![]() 存在实数
存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ,且
,且![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
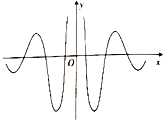
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(注意:在试题卷上作答无效)
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止;
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
求依方案甲所需化验次数不少于依方案乙所需化验次数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】仔细观察数列给出部分的数字,寻找规律,在空白处填上合适的数字.
(1)2,3,5,8,__________21;(2)8,_______14,17,20,23;
(3)2,4,8,16,_______,64;(4)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,_________.
,_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
, ![]() 为
为![]() 上一点,
上一点,![]() 为菱形
为菱形![]() 对角线的交点.
对角线的交点.
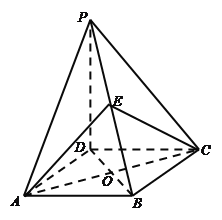
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,四棱锥
,四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com