
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
【答案】(1)a≥1;(2)函数f(x)在(0,2π)上有且仅有唯一的极大值点,无极小值点;理由详见解析
【解析】
(1)只需h′(x)≥0在(0,+∞)恒成立,借助于三角函数的有界性,问题可解决.
(2)分x∈(0,1),![]() ,
,![]() ,
,![]() 四种情形分别研究f(x)的单调性,进而得出结论.
四种情形分别研究f(x)的单调性,进而得出结论.
解:(1)∵![]() ,
,
∴![]() ax+cosx,因为h(x)是(0,+∞)上的单调递增函数,
ax+cosx,因为h(x)是(0,+∞)上的单调递增函数,
∴h′(x)=a﹣sinx≥0(x>0)恒成立,因为sinx∈[﹣1,1],
故a≥1时,h′(x)≥0恒成立,且导数为0时不连续.
故a≥1即为所求.
(2)由(1)知,![]() ,
,
①当x∈(0,1]时,f′(x)≥1﹣cosx>0,
此时函数f(x)单调递增,无极值点;
②当![]() 时,则
时,则![]() ,
,
∵![]() ,而由三角函数的性质可知,
,而由三角函数的性质可知,![]() ,
,
∴![]() ,
,
此时函数f(x)单调递增,无极值点;
③当![]() 时,cosx<0,则
时,cosx<0,则![]() ,
,
此时函数f(x)单调递增,无极值点;
④当![]() 时,令
时,令![]() ,则
,则![]() ,
,
∴函数g(x)单调递减,
又![]() ,
,
∴存在唯一的![]() ,使得g(x0)=0,
,使得g(x0)=0,
且当![]() 时,g(x)=f′(x)>0,f(x)单调递增,
时,g(x)=f′(x)>0,f(x)单调递增,
当x∈(x0,2π)时,g(x)=f′(x)<0,f(x)单调递减,
故x0是函数f(x)的极大值点,
综上所述,函数f(x)在(0,2π)上有且仅有唯一的极大值点,无极小值点.


科目:高中数学 来源: 题型:
【题目】若有平面![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则下列命题中真命题的序号有________.(1)过点
,则下列命题中真命题的序号有________.(1)过点![]() 且垂直于
且垂直于![]() 的直线平行于
的直线平行于![]() ;(2)过点
;(2)过点![]() 且垂直于
且垂直于![]() 的平面垂直于
的平面垂直于![]() ;(3)过点
;(3)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内;(4)过点
内;(4)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内.
内.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,向量
是坐标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,现沿对角线
,现沿对角线![]() 将
将![]() 折起,使点A到达点P,点M,N分别在直线
折起,使点A到达点P,点M,N分别在直线![]() ,
,![]() 上,且A,B,M,N四点共面.
上,且A,B,M,N四点共面.
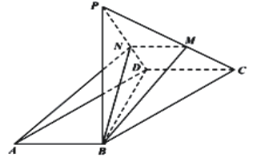
(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小为
平面角大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2ax﹣lnx﹣1,a∈R.
(1)当a![]() 时,求f(x)的单调区间及极值;
时,求f(x)的单调区间及极值;
(2)若a为整数,且不等式f(x)≥x对任意x∈(0,+∞)恒成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查,为此需要抽验960人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案①:将每个人的血分别化验,这时需要验960次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次;否则,若呈阳性,则需对这
个人的血就只需检验一次;否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这样,该组
个人的血样再分别进行一次化验,这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() ,试比较方案②中,
,试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数).
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com