
����Ŀ��ij����˾Ϊ����ʵ����Ա���Ľ�����ȫ���᳹���������߹��������Ҫ������ȫ��˾��Χ�ھ���һ���Ҹ��ղ飬Ϊ����Ҫ����960�˵�Ѫ�����л��飬���������϶࣬���߲����ƶ����������ֿɹ�ѡ��ķ���.
�����٣���ÿ���˵�Ѫ�ֱ��飬��ʱ��Ҫ��960��.
�����ڣ���![]() ����һ�����������飬�Ѵ�ÿ��
����һ�����������飬�Ѵ�ÿ��![]() ���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���
���˳�����Ѫ�����һ����м��飬���ÿ���˵�Ѫ��Ϊ���ԣ�������Ľ�������ԣ���![]() ���˵�Ѫ��ֻ�����һ�Σ������������ԣ��������
���˵�Ѫ��ֻ�����һ�Σ������������ԣ��������![]() ���˵�Ѫ���ٷֱ����һ�λ��飬����������
���˵�Ѫ���ٷֱ����һ�λ��飬����������![]() ���˵�Ѫ�ܹ���Ҫ����
���˵�Ѫ�ܹ���Ҫ����![]() ��.
��.
����˴��ղ���ÿ���˵�Ѫ����������Եĸ���Ϊ![]() ������Щ��֮������鷴Ӧ�����.
������Щ��֮������鷴Ӧ�����.
��1���跽�����У�ij��![]() ������ÿ���˵�Ѫ�������Ϊ
������ÿ���˵�Ѫ�������Ϊ![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
��2����![]() ���ԱȽϷ������У�
���ԱȽϷ������У�![]() �ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ�(������������뱣������).
�ֱ�ȡ2��3��4ʱ�����軯���ƽ���ܴ�������ָ���������ַ�������£���ȷ����٣��������������ƽ�����ٶ��ٴΣ�(������������뱣������).
���𰸡���1����������2��390��
��������
��1����ÿ���˵�Ѫ�����Է�Ӧ�ĸ���Ϊ![]() ����
����![]() ��
��![]() �����
�����![]() ���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ��ʣ������Է�Ӧ�ĸ��ʵ÷ֲ��У�
���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ��ʣ������Է�Ӧ�ĸ��ʵ÷ֲ��У�
��2���ɣ�1�����������![]() ����
����![]() �ֱ�������ֵ��ɵü���������Ӷ��ɵý��ۣ�
�ֱ�������ֵ��ɵü���������Ӷ��ɵý��ۣ�
��1����ÿ���˵�Ѫ�����Է�Ӧ�ĸ���Ϊ![]() ����
����![]()
����![]() ���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ���Ϊ
���˵�Ѫ��Ϻ�����Է�Ӧ�ĸ���Ϊ![]() �������Է�Ӧ�ĸ���Ϊ
�������Է�Ӧ�ĸ���Ϊ![]()
�������֪![]() ������
������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
��2����������
��ϣ�1��֪ÿ���˵�ƽ���������Ϊ��
![]()
���Ե�![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ����Ҫ������ܴ�
����Ҫ������ܴ�
��Ϊ![]() �Σ�
�Σ�
![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ����Ҫ������ܴ���Ϊ
����Ҫ������ܴ���Ϊ![]() �Σ�
�Σ�
![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ����Ҫ����Ĵ�����Ϊ
����Ҫ����Ĵ�����Ϊ![]() ��
��
��![]() ʱ���������࣬
ʱ���������࣬![]() ʱ�������У�
ʱ�������У�![]() ʱ�����������
ʱ�����������
�����÷��������軯��![]() �Σ�
�Σ�
�������ַ�������£���ȷ����٣���![]() ʱ�������������ƽ��
ʱ�������������ƽ��
����![]() ��
�Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����lnx��sinx,��f��x���ĵ�����Ϊf'��x��.
��1����h��x����ax![]() f'��x���ǣ�0,+�ޣ��ϵĵ�����������,��ʵ��a��ȡֵ��Χ��
f'��x���ǣ�0,+�ޣ��ϵĵ�����������,��ʵ��a��ȡֵ��Χ��
��2����x����0,2����,���жϺ���f��x���ļ�ֵ�����,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊʵ�ֹ����������������ķ�չս��Ŀ�꣬���ҼӴ��˷�ƶ���������.ij������2015 ����ǰ�������ƶ�ʣ�����ƶ���Ļ���ռ����ƶ���������ıȣ�Ϊ![]() .2015�꿪ʼ��ȫ��ʵʩ������ƶ�����ߺ�ƶЧ��������ߣ�����2019���ʵʩ�ķ�ƶ��Ŀ������Ŀ�μӻ���ռ�ȣ��μӸ���Ŀ����ռ 2019 ��ƶ���������ıȣ�������Ŀ����ƶ�ʼ��±���
.2015�꿪ʼ��ȫ��ʵʩ������ƶ�����ߺ�ƶЧ��������ߣ�����2019���ʵʩ�ķ�ƶ��Ŀ������Ŀ�μӻ���ռ�ȣ��μӸ���Ŀ����ռ 2019 ��ƶ���������ıȣ�������Ŀ����ƶ�ʼ��±���
ʵʩ��Ŀ | ��ֲҵ | ��ֳҵ | ������ҵ | ����ҵ |
�μ��û��� |
|
|
|
|
��ƶ�� |
|
|
|
|
��ô![]() �������ƶ����ʵʩ������ƶ������ǰ�������ƶ�ʵģ� ��
�������ƶ����ʵʩ������ƶ������ǰ�������ƶ�ʵģ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijУ��֯��һ������Ͷ�������У�����һ��һ�����������£���ij��ij��Ͷ�����У�����������Ͷ���������ɶԷ�����Ͷ��. ���ɼס������˽���һ��һͶ������������ÿ��Ͷ�����еĸ��ʷֱ���![]() ��
��![]() .���˹�Ͷ��3�Σ��ҵ�һ���ɼ�ʼͶ��. ����ÿ��ÿ��Ͷ��������������Ӱ��.��3��Ͷ�����������Ǽס��ס��ҵĸ���___________��
.���˹�Ͷ��3�Σ��ҵ�һ���ɼ�ʼͶ��. ����ÿ��ÿ��Ͷ��������������Ӱ��.��3��Ͷ�����������Ǽס��ס��ҵĸ���___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽ�������������߲��Դ��в���ũҩ��ʳ��ʱ��Ҫ��ϴ���Σ�ͳ�Ʊ��е�![]() ��ʾ��ϴ�Ĵ�����
��ʾ��ϴ�Ĵ�����![]() ��ʾ��ϴ
��ʾ��ϴ![]() �κ�
�κ�![]() ǧ�˸��߲˲�����ũҩ������λ���ˣ���
ǧ�˸��߲˲�����ũҩ������λ���ˣ���
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
��1������ͼ������ϵ�У����ɢ��ͼ��������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ��ϴ
��һ��������Ϊ��ϴ![]() �κ�
�κ�![]() ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
ǧ�˸��߲˲�����ũҩ���Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�

��2�������жϼ���������е����ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
����![]() ��
��![]() ��
��
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
��3��������Ļع鷽�̽��вв������
���������Իع鷽��![]() ��ϵ�����㹫ʽ�ֱ�Ϊ
��ϵ�����㹫ʽ�ֱ�Ϊ ��
��![]() ��
��
�� ��
��![]() ˵��ģ��Ч���dz��ã�
˵��ģ��Ч���dz��ã�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ij���Ͳ�����ij���л������з��������������磬Ϊ�Ƚ����������Ч����ѡȡ100��־Ը�ߣ�����������ֳ����飬ÿ��50��.��һ��־Ը��ע��������磬�ڶ���־Ը��ע���������磬����һ��ʱ�����100��־Ը�߽��и����Ͳ��������⣬������![]() ��־Ը��δ���������Ͳ������壬��δ���������Ͳ��������־Ը���У�ע����������־Ը��ռ
��־Ը��δ���������Ͳ������壬��δ���������Ͳ��������־Ը���У�ע����������־Ը��ռ![]() .
.
�������� | δ�������� | �ϼ� | |
�� | |||
�� | |||
�ϼ� |
��1�������������ݣ������������
��2�����ݣ�1���е����������ж��ܷ���![]() �İ�����Ϊ�������������Ч���в���.
�İ�����Ϊ�������������Ч���в���.
�ο���ʽ��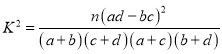 ������
������![]() .
.
�ο����ݣ�
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У��ı���
�У��ı���![]() Ϊƽ���ı��Σ�������
Ϊƽ���ı��Σ�������![]() Ϊ�ȱ������Σ���֪
Ϊ�ȱ������Σ���֪![]() ��
��![]() ��
��![]() ��
��![]() .
.
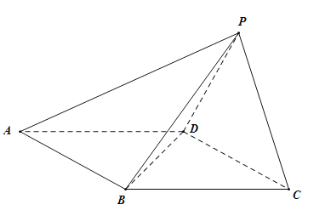
��1����֤��![]()
��2����ֱ��![]() ����
����![]() ���ɵĽǵ�����ֵ.
���ɵĽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������1������ƽ��ǵĴ�СΪ60����A��B��1�ϵ��������㣬��AB��2��C������D����������AB��ƽ��BCD���ɵĽ�Ϊ30�����ҵ�A��ƽ��BCD�ϵ���ӰH�ڡ�BCD���ڲ��������߽磩�����H�Ĺ켣�ij��ȵ��ڣ� ��
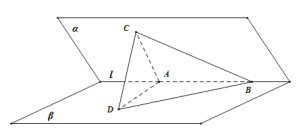
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ����������乤�̰���������Դ���Ʊ�Ϊ�������ƣ�ʵ��������Դ�����빩���Ķ������νӣ����̽���Ҳ�ӿ������������ߵ����ľ��÷�չ�����ܵ����̽����У�ij�ιܵ�����Ҫ����һ��Ͽ�ȣ�Ͽ����ǡ����һ��ֱ�ǹսǣ�ˮƽ�����ƶ������ܾ����˹սǣ��ӿ�Ϊ![]() ��Ͽ�ȹ����Ϊ
��Ͽ�ȹ����Ϊ![]() ��Ͽ�ȣ���ͼ��ʾ��λ��Ͽ�����±�������
��Ͽ�ȣ���ͼ��ʾ��λ��Ͽ�����±�������![]() ��
��![]() ������ǡ�þ����ս��ڲඥ��
������ǡ�þ����ս��ڲඥ��![]() ����
����![]() ��
��![]() ��
��![]() ��ͬһˮƽ���ڣ�����
��ͬһˮƽ���ڣ�����![]() ��Ͽ���Ͽ�����±����ɽ�Ϊ
��Ͽ���Ͽ�����±����ɽ�Ϊ![]() ����
����![]() �ij�Ϊ________����
�ij�Ϊ________����![]() ��ʾ���ף�Ҫʹ������˳��ͨ���սǣ��䳤�Ȳ��ܵ���________�ף�
��ʾ���ף�Ҫʹ������˳��ͨ���սǣ��䳤�Ȳ��ܵ���________�ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com