
已知函数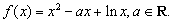
(I)若函数 在
在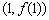 处的切线垂直于
处的切线垂直于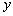 轴,求实数a的值;
轴,求实数a的值;
(II) 在(I)的条件下,求函数 的单调区间;
的单调区间;
(III) 若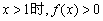 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(I)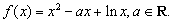 定义域为
定义域为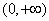
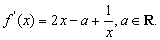
依题意,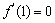 .
.
所以 ,解得
,解得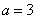 ……………4分
……………4分
(II)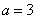 时,
时,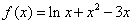 ,定义域为
,定义域为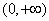 ,
,
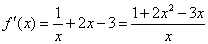
当 或
或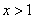 时,
时,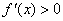 ,
,
当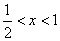 时,
时,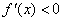 ,
,
故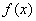 的单调递增区间为
的单调递增区间为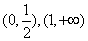 ,单调递减区间为
,单调递减区间为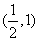 .----8分
.----8分
(III)解法一:由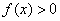 ,得
,得 在
在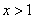 时恒成立,
时恒成立,
令 ,则
,则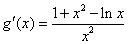
令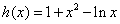 ,则
,则
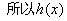 在
在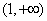 为增函数,
为增函数,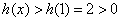 .
.
故 ,故
,故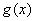 在
在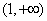 为增函数.
为增函数. 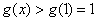 ,
,
所以 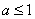 ,即实数
,即实数 的取值范围为
的取值范围为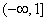 . ……………13分
. ……………13分
解法二: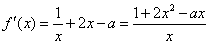
令 ,则
,则 ,
,
(i)当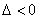 ,即
,即 时,
时,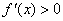 恒成立,
恒成立,
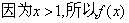 在
在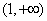 上单调递增,
上单调递增,
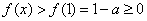 ,即
,即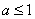 ,所以
,所以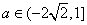 ;
;
(ii)当 ,即
,即 时,
时,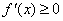 恒成立,
恒成立,
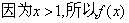 在
在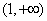 上单调递增,
上单调递增,
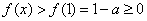 ,即
,即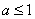 ,所以
,所以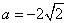 ;
;
(iii)当 ,即
,即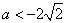 或
或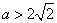 时,
时,
方程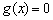 有两个实数根
有两个实数根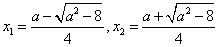
若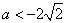 ,两个根
,两个根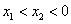 ,
,
当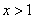 时,
时,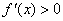 ,
,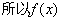 在
在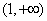 上单调递增,
上单调递增,
则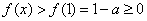 ,即
,即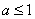 ,所以
,所以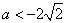 ;
;
若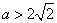 ,
,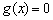 的两个根
的两个根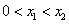 ,
,
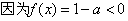 ,且
,且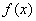 在
在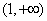 是连续不断的函数
是连续不断的函数
所以总存在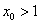 ,使得
,使得 ,不满足题意.
,不满足题意.
综上,实数 的取值范围为
的取值范围为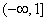 . ……………13分
. ……………13分


科目:高中数学 来源: 题型:
某班举行联欢会由5个节目组成,演出顺序有如下要求:节目甲必须和节目乙相邻,
且节目甲不能排在第一个和最后一个,则该班联欢会节目演出顺序的编排方案共有___________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
向量a=(cos 23°,cos 67°),向量b=(cos 68°,cos 22°).
(1)求a·b;
(2)若向量b与向量m共线,u=a+m,求u的模的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com