
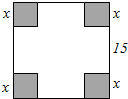
 如图,有一块边长为15cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
如图,有一块边长为15cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.分析 (1)利用柱体的体积计算公式求出盒子的体积y关于x的函数关系式和x的取值范围;
(2)由题意可得x(15-2x)2=150,(0<x<$\frac{15}{2}$).令f(x)=4x3-60x2+225x,可得f′(x)=12x2-120x+225=(6x-15)(2x-15),利用导数研究其单调性极值与最值,再利用二分法求出其零点即可.
解答 解:(1)∵截去的小正方形的边长为xcm,
∴折成的无盖盒子底面是边长为(15-2x)cm的正方形,高是xcm.
∴盒子的体积y=x(15-2x)2,(0<x<$\frac{15}{2}$).
(2)x(15-2x)2=150,(0<x<$\frac{15}{2}$).
令f(x)=4x3-60x2+225x,
f′(x)=12x2-120x+225=(6x-15)(2x-15),
由f′(x)>0,解得$0<x<\frac{5}{2}$,此时函数f(x)单调递增;由f′(x)<0,解得$\frac{5}{2}<x<\frac{15}{2}$,此时函数f(x)单调递减.
∴当x=$\frac{5}{2}$时,函数f(x)取得最大值:$f(\frac{5}{2})$=$4×(\frac{5}{2})^{3}$-$60×(\frac{5}{2})^{2}$+225×$\frac{5}{2}$=250.
由f(0)=0,f(1)=169,利用二分法可得:$f(\frac{1}{2})$=98,$f(\frac{3}{4})$≈137,$f(\frac{7}{8})$≈143.5,$f(\frac{15}{16})$≈161.5,$f(\frac{29}{32})$≈157,$f(\frac{57}{64})$≈155.6,$f(\frac{113}{128})$≈154.62,$f(\frac{225}{256})$≈
154.1,$f(\frac{449}{512})$≈153.87,$f(\frac{897}{1024})$≈153.7,$f(\frac{1793}{2048})$≈153.6,$f(\frac{3585}{4096})$≈153.6,$f(\frac{7169}{8192})$≈153.6,
取零点$\frac{7169}{8192}$≈0.9.
又$f(\frac{15}{2})$=0,
因此函数f(x)只有一个零点约为0.9.
点评 本题考查了将实际问题转化为数学问题的能力\利用导数研究函数性质、求函数在开区间上的最值的方法、二分法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定等于0 | B. | 一定小于0 | C. | 一定大于0 | D. | 符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com