
【题目】已知集合 ![]() ,分别求适合下列条件的实数a的值.
,分别求适合下列条件的实数a的值.
(1)![]() ;
;
(2)![]() .
.
【答案】
(1)解:因为 ![]() ,所以9∈A且9∈B.
,所以9∈A且9∈B.
故2a-1=9或a2=9,解得a=5或a=±3.
经检验知,a=5或 ![]() 满足题意,a=3不满足题意,舍去.
满足题意,a=3不满足题意,舍去.
所以a=5或 ![]()
(2)解:因为 ![]() ,所以9∈(A∩B),
,所以9∈(A∩B),
由(1)知a=5或 ![]() .
.
当a=5时, ![]() ,此时
,此时 ![]() ,这与A∩B={9}矛盾,舍去;
,这与A∩B={9}矛盾,舍去;
当 ![]() 时,
时, ![]() ,此时A∩B={9},满足题意.
,此时A∩B={9},满足题意.
所以 ![]()
【解析】(1)中只说明9是A ∩ B 中的元素,则9同时是A,B中的元素,从而求出a的值,要注意元素的互异性.
(2)中说明9中A ∩ B 中唯一的元素,没有其它元素,从而求出a的值,要注意元素的互异性.
【考点精析】解答此题的关键在于理解元素与集合关系的判断的相关知识,掌握对象![]() 与集合
与集合![]() 的关系是
的关系是![]() ,或者
,或者![]() ,两者必居其一,以及对集合的特征的理解,了解集合中的元素具有确定性、互异性和无序性.
,两者必居其一,以及对集合的特征的理解,了解集合中的元素具有确定性、互异性和无序性.


科目:高中数学 来源: 题型:
【题目】将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )
A.![]()
B.![]()
C.36
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex﹣ax2 , g(x)是f(x)的导函数. (I)求g(x)的极值;
(II)证明:对任意实数x∈R,都有f′(x)≥x﹣2ax+1恒成立:
(Ⅲ)若f(x)≥x+1在x≥0时恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?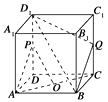
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣π<φ<0)在区间 ![]() 上单调递增,且函数值从﹣2增大到0.若
上单调递增,且函数值从﹣2增大到0.若 ![]() ,且f(x1)=f(x2),则f(x1+x2)=( )
,且f(x1)=f(x2),则f(x1+x2)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个正方体的玩具,六个面标注了数字1,2,3,4,5,6,甲、乙两位学生进行如下游戏:甲先抛掷一次,记下正方体朝上的数字 ![]() ,再由乙抛掷一次,记下正方体朝上数字
,再由乙抛掷一次,记下正方体朝上数字 ![]() ,若
,若 ![]() 就称甲、乙两人“默契配合”,则甲、乙两人“默契配合”的概率为( )
就称甲、乙两人“默契配合”,则甲、乙两人“默契配合”的概率为( )
A.![]()
B.![]()
C.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长都相等的四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,则下面四个结论中不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面ABC
D.平面PAE⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com