
 如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=1,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD,如图(2).
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=1,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD,如图(2).分析 (Ⅰ)由条件可得EF∥CD∥AB,利用直线和平面平行的判定定理证得EF∥平面PAB.同理可证,EG∥平面PAB,可得平面EFG∥平面PAB.再利用两个平面平行的性质可得AP∥平面EFG.
(Ⅱ)证明EF⊥平面PAD,即可证明:平面PAD⊥平面EFG;
(Ⅲ)根据VC-EFG=VG-CEF=$\frac{1}{3}$•S△CEF•CG,运算求得结果.
解答 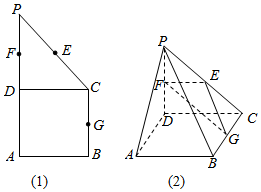 (Ⅰ)证明:∵E、F分别是PC、PD的中点,
(Ⅰ)证明:∵E、F分别是PC、PD的中点,
∴EF∥CD∥AB,
又EF?平面PAB,AB?平面PAB,
∴EF∥平面PAB.
同理,EG∥平面PAB,
∵EF∩EG=E,
∴∴平面EFG∥平面PAB,
又AP?平面PAB,∴AP∥平面EFG…4分
(Ⅱ)证明:∵CD⊥PD,CD⊥AD,PD∩AD=D,
∴CD⊥平面PAD,
又E、F分别是PC、PD的中点的中点
∴EF∥CD,
∴EF⊥平面PAD,
又EF?平面EFG,
则平面PAD⊥平面EFG…8分
(3)解:${V_{C-EFG}}={V_{G-CEF}}=\frac{1}{3}{S_{△CEF}}.GC$=$\frac{1}{3}×\frac{1}{8}×\frac{1}{2}=\frac{1}{48}$…12分.
点评 本题主要考查直线和平面平行的判定定理、平面和平面垂直的判定定理的应用,用等体积法求棱锥的体积,属于中档题.


科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=4 | B. | m≠4 | C. | m≠-1 | D. | m∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (C${\;}_{26}^{1}$)2A${\;}_{10}^{2}$ | B. | A${\;}_{26}^{2}$A${\;}_{10}^{2}$ | C. | (C${\;}_{26}^{1}$)2102 | D. | A${\;}_{26}^{2}$102 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com