已知数列{an},a1=1,an=λan-1+λ-2(n≥2).
(1)当λ为何值时,数列{an}可以构成公差不为零的等差数列,并求其通项公式;
(2)若λ=3,求数列{an}的通项公式an.
解:(1)a
2=λa
1+λ-2=2λ-2,a
3=λa
2+λ-2=2λ
2-2λ+λ-2=2λ
2-λ-2,
∵a
1+a
3=2a
2,∴1+2λ
2-λ-2=2(2λ-2),得2λ
2-5λ+3=0,解得λ=1或λ=

.
当λ=

时,a
2=2×

-2=1,a
1=a
2,故λ=

不合题意舍去;
当λ=1时,代入a
n=λa
n-1+λ-2可得a
n-a
n-1=-1,
∴数列{a
n}构成首项为a
1=1,d=-1的等差数列,
∴a
n=2-n.
(2)当λ=3时,a
n=3a
n-1+1,即a
n+

=3(a
n-1+

),
令b
n=a
n+

即b
n=3b
n-1,
∴数列{b
n}构成首项为b
1=

,公比为3的等比数列,
∴b
n=

×3
n-1=
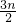
,
∴a
n=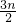
-

分析:(1)根据a
n=λa
n-1+λ-2,可得a
2,a
3的值,利用数列{a
n}可以构成公差不为零的等差数列,可求λ的值,从而可求数列的通项公式;
(2)当λ=3时,a
n=3a
n-1+1,即a
n+

=3(a
n-1+

),构造新数列b
n=a
n+

,可得数列{b
n}构成首项为b
1=

,公比为3的等比数列,从而可求数列{a
n}的通项公式a
n.
点评:本题考查等差数列的定义,考查构造法证明等比数列,解题的关键是对递推式进行变形,构造等比数列模型.

 .
. 时,a2=2×
时,a2=2× -2=1,a1=a2,故λ=
-2=1,a1=a2,故λ= 不合题意舍去;
不合题意舍去; =3(an-1+
=3(an-1+ ),
), 即bn=3bn-1,
即bn=3bn-1, ,公比为3的等比数列,
,公比为3的等比数列, ×3n-1=
×3n-1=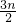 ,
,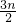 -
-
 =3(an-1+
=3(an-1+ ),构造新数列bn=an+
),构造新数列bn=an+ ,可得数列{bn}构成首项为b1=
,可得数列{bn}构成首项为b1= ,公比为3的等比数列,从而可求数列{an}的通项公式an.
,公比为3的等比数列,从而可求数列{an}的通项公式an.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案