
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
| A.分析法 |
| B.综合法 |
| C.分析法和综合法综合使用 |
| D.间接证法 |
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:单选题
如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…),
则在第n个图形中共有( )个顶点。
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. +3n+8 +3n+8 | D.12n |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:若整数系数的一元二次方程 有有理实数根,那么
有有理实数根,那么 ,
, ,
, 中至少有一个是偶数,下列假设中正确的是( )
中至少有一个是偶数,下列假设中正确的是( )
A.假设 , , , , 都是偶数 都是偶数 |
B.假设 , , , , 都不是偶数 都不是偶数 |
C.假设 , , , , 至多有一个是偶数 至多有一个是偶数 |
D.假设 , , , , 至多有两个偶数 至多有两个偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
实验中学“数学王子”张小明在自习课上,对正整数1,2,3,4, 按如下形式排成数阵好朋友王大安问他“由上而下第20行中从左到右的第三个数是多少”张小明自上而下逐个排了两节课,终于找到了这个数,聪明的你一定知道这个数是( ) 
| A.190 | B.191 | C.192 | D.193 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题“三角形的内角中至少有一个角不大于 ”时,反设正确的是
”时,反设正确的是
A.假设三个内角都不大于 | B.假设三个内角都大于 |
C.假设三个内角至多有一个大于 | D.假设三个内角至多有二个大于 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察分析下表中的数据:
| 多面体 | 面数(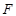 ) ) | 顶点数(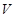 ) ) | 棱数(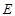 ) ) |
| 三棱锥 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体 | 6 | 8 | 12 |
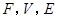 所满足的等式是_________.
所满足的等式是_________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 |
| C.86 | D.92 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①~⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体,则下列选择方案中,能够完成任务的为( )
| A.模块①,②,⑤ | B.模块①,③,⑤ |
| C.模块②,④,⑤ | D.模块③,④,⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列推理中属于归纳推理且结论正确的是( )
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆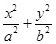 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com