Ϊ�˽�ij��ѧ��ϲ���������Ƿ����Ա��йأ��Ա���50�˽������ʾ�����õ������µ���������
|
ϲ�������� |
��ϲ�������� |
�ϼ� |
| ���� |
|
5 |
|
| �� |
10 |
|
|
| �ϼ� |
|
|
50 |
��֪��ȫ��50���������ȡ1�˳鵽ϲ���������ѧ���ĸ���Ϊ
��
��1���뽫���������������������
��2���Ƿ���99.5%�İ�����Ϊϲ�����������Ա��йأ�˵��������ɣ�
��3����֪ϲ���������10λŮ���У�A
1��A
2��A
3��ϲ������ë��B
1��B
2��ϲ����ƹ����C
1��C
2��ϲ�����������ٴ�ϲ������ë��ϲ����ƹ����ϲ���������Ů���и�ѡ��1��������������ĵ��飬��B
1��C
1��ȫ��ѡ�еĸ��ʣ�
������ٽ�ֵ�����ο���
| p��K2��k�� |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
���ο���ʽ��K
2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
������n=a+b+c+d��



 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
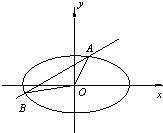 ֱ��y=kx+b������x2+4y2-4=0����A��B���㣬�ǡ�AOB�����ΪS��O������ԭ�㣩��
ֱ��y=kx+b������x2+4y2-4=0����A��B���㣬�ǡ�AOB�����ΪS��O������ԭ�㣩��