
【题目】设函数![]() ,已知曲线
,已知曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行
平行
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在自然数![]() ,使得方程
,使得方程![]() 在
在![]() 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
(Ⅲ)设函数![]() (
(![]() 表示
表示![]() 中的较小者),求
中的较小者),求![]() 的最大值。
的最大值。
【答案】(1) ![]() .
.
(2) ![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.证明见解析.
内存在唯一的根.证明见解析.
(3) ![]() .
.
【解析】试题分析:(Ⅰ)求出f(x)的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得![]() ;(Ⅱ)求出
;(Ⅱ)求出![]() 的导数和单调区间,最值,由零点存在定理,即可判断存在
的导数和单调区间,最值,由零点存在定理,即可判断存在![]() ;(Ⅲ)由(Ⅱ)求得
;(Ⅲ)由(Ⅱ)求得![]() 的解析式,通过
的解析式,通过![]() 的最大值,即可得到所求.
的最大值,即可得到所求.
试题解析:(Ⅰ)由题意知,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,所以
,所以![]() ,
,
又![]() 所以
所以![]() .
.
(Ⅱ)![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.
内存在唯一的根.
设![]()
当![]() 时,
时, ![]() .
.
又![]()
所以存在![]() ,使
,使![]() .
.
因为![]() 所以当
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 单调递增.
单调递增.
所以![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.
内存在唯一的根.
(Ⅲ)由(Ⅱ)知,方程![]() 在
在![]() 内存在唯一的根
内存在唯一的根![]() ,且
,且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以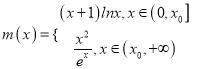 .
.
当![]() 时,若
时,若![]()
若![]() 由
由![]() 可知
可知![]() 故
故![]()
当![]() 时,由
时,由![]() 可得
可得![]() 时,
时, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() 单调递减;
单调递减;
可知![]() 且
且![]() .
.
综上可得函数![]() 的最大值为
的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)请估计该市公众对“车辆限行”的赞成率和被调查者的年龄平均值;
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若在这50名被调查者中随机发出20份的调查问卷,记![]() 为所发到的20人中赞成“车辆限行”的人数,求使概率
为所发到的20人中赞成“车辆限行”的人数,求使概率![]() 取得最大值的整数
取得最大值的整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exsinx.
(1)求函数f(x)的单调区间;
(2)如果对于任意的 ![]() ,f(x)≥kx恒成立,求实数k的取值范围;
,f(x)≥kx恒成立,求实数k的取值范围;
(3)设函数F(x)=f(x)+excosx, ![]() ,过点
,过点 ![]() 作函数F(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和的值.
作函数F(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{xn},求数列{xn}的所有项之和的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求实数![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 存在零点,求实数
存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若函数
,若函数![]() 与
与![]() 的图像只有一个公共点,求实数
的图像只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数据显示,某![]() 公司2018年上半年五个月的收入情况如下表所示:
公司2018年上半年五个月的收入情况如下表所示:
月份 | 2 | 3 | 4 | 5 | 6 |
月收入(万元) | 1.4 | 2.56 | 5.31 | 11 | 21.3 |
根据上述数据,在建立该公司2018年月收入![]() (万元)与月份
(万元)与月份![]() 的函数模型时,给出两个函数模型
的函数模型时,给出两个函数模型![]() 与
与![]() 供选择.
供选择.
(1)你认为哪个函数模型较好,并简单说明理由;
(2)试用你认为较好的函数模型,分析大约从第几个月份开始,该公司的月收入会超过100万元?(参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:
组别 | 文科 | 理科 | ||
性别 | 男生 | 女生 | 男生 | 女生 |
人数 | 3 | 1 | 3 | 2 |
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮.某公司研发的![]() ,
,![]() 两种芯片都已经获得成功.该公司研发芯片已经耗费资金
两种芯片都已经获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产.经市场调查与预测,生产
千万元,现在准备投入资金进行生产.经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式;
(千万元)的函数关系式;
(2)如果公司只生产一种芯片,生产哪种芯片毛收入更大?
(3)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() ,
,![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所过利润,当
表示公司所过利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有![]() 间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
每间客房的定价 | 220元 | 200元 | 180元 | 160元 |
每天的入住率 |
|
|
|
|
对于每间客房,若有客住,则成本为80元;若空闲,则成本为40元.要使此宾馆每天的住房利润最高,则每间客房的定价大致应为( )
A. 220元 B. 200元 C. 180元 D. 160元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com